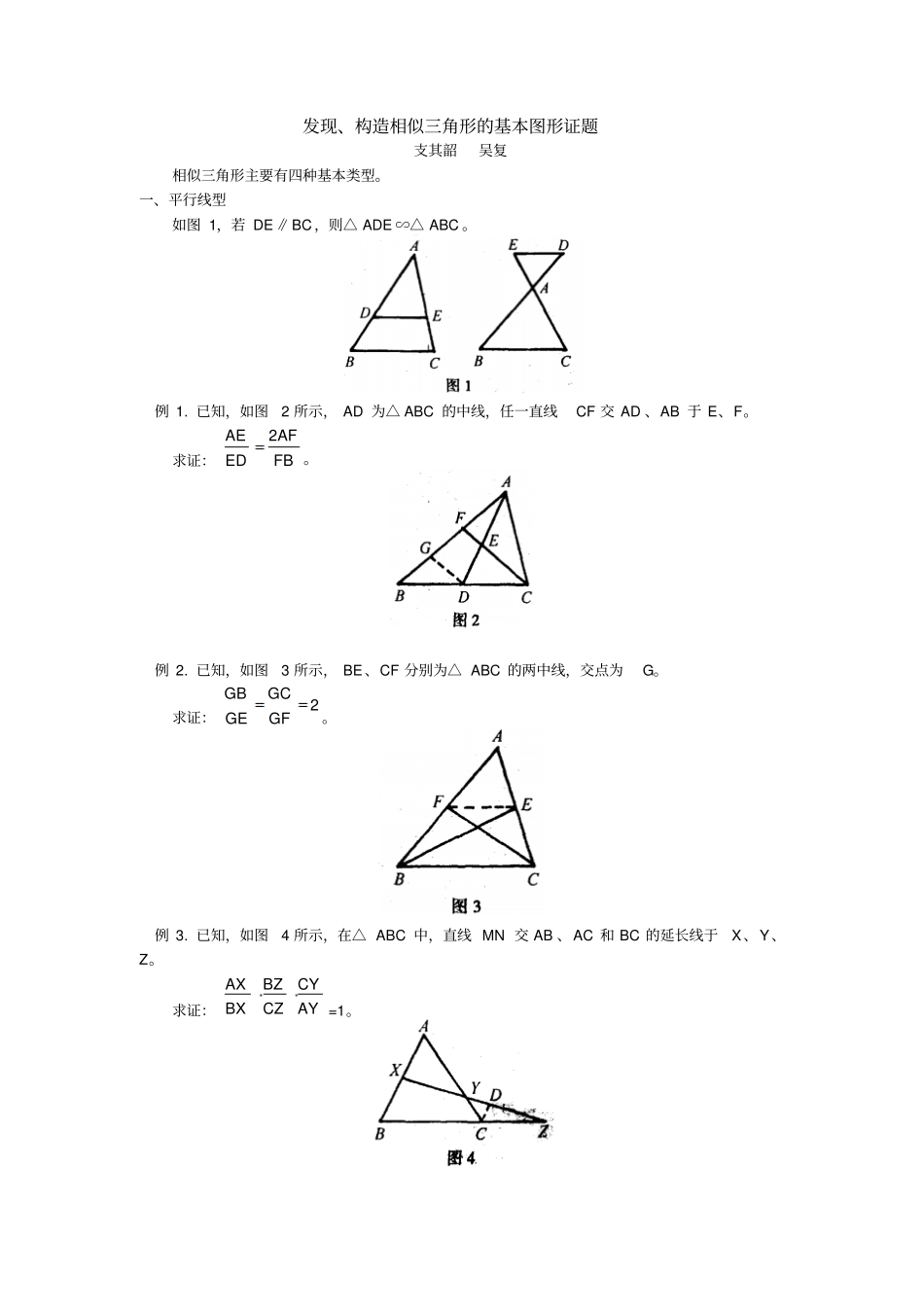
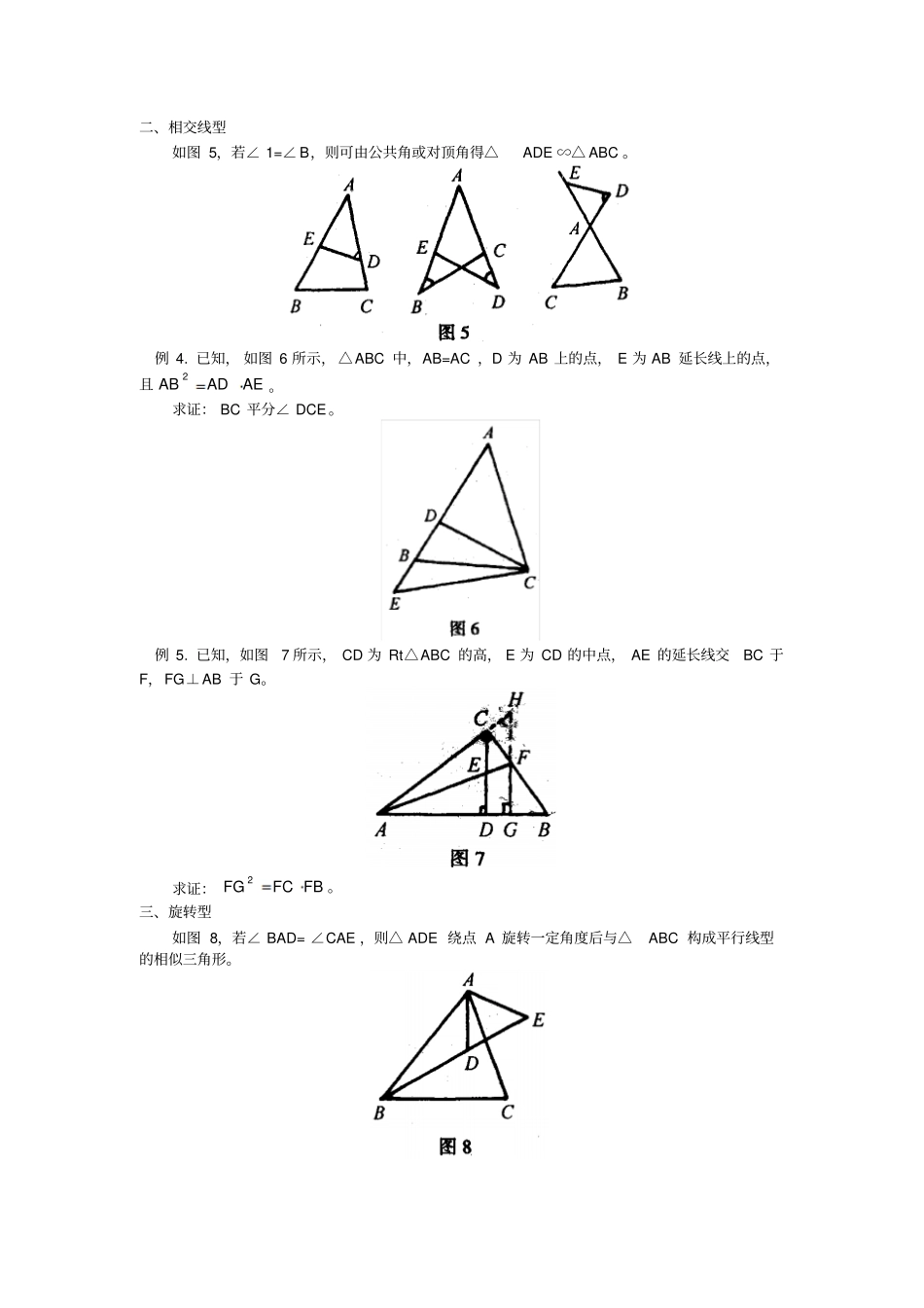
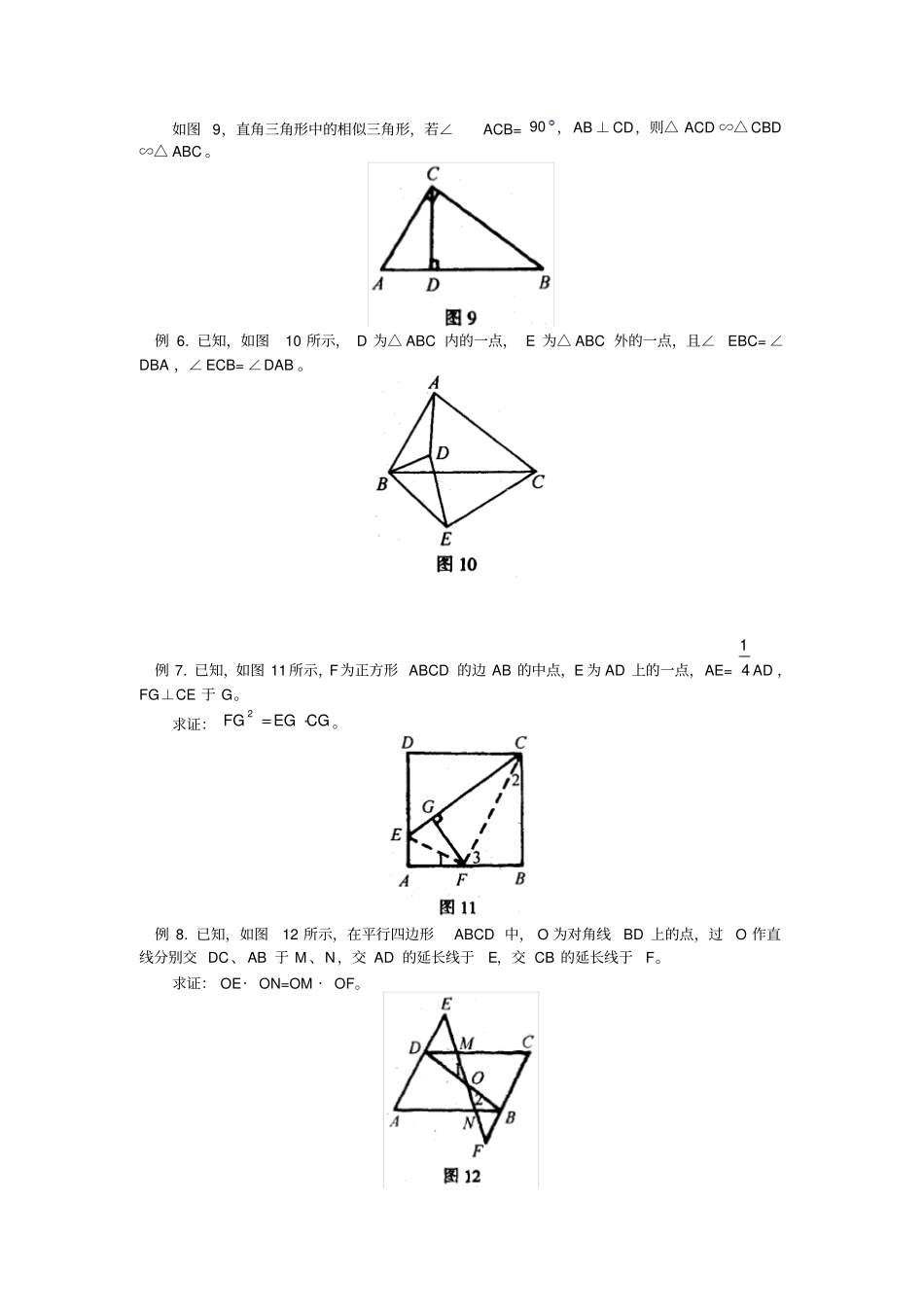
发现、构造相似三角形的基本图形证题支其韶吴复相似三角形主要有四种基本类型。一、平行线型如图 1,若 DE∥BC,则△ ADE ∽△ ABC 。例 1. 已知,如图2 所示, AD 为△ ABC 的中线,任一直线CF 交 AD 、AB 于 E、F。求证:FBAF2EDAE。例 2. 已知,如图3 所示, BE、CF 分别为△ ABC 的两中线,交点为G。求证:2GFGCGEGB。例 3. 已知,如图4 所示,在△ ABC 中,直线 MN 交 AB 、AC 和 BC 的延长线于X、Y、Z。求证:AYCYCZBZBXAX=1。二、相交线型如图 5,若∠ 1=∠ B,则可由公共角或对顶角得△ADE ∽△ ABC 。例 4. 已知, 如图 6 所示, △ABC 中,AB=AC ,D 为 AB 上的点, E 为 AB 延长线上的点,且AEADAB2。求证: BC 平分∠ DCE 。例 5. 已知,如图7 所示, CD 为 Rt△ABC 的高, E 为 CD 的中点, AE 的延长线交BC 于F,FG⊥AB 于 G。求证:FBFCFG2。三、旋转型如图 8,若∠ BAD= ∠CAE ,则△ ADE 绕点 A 旋转一定角度后与△ABC 构成平行线型的相似三角形。如图 9,直角三角形中的相似三角形,若∠ACB= 90 ,AB ⊥ CD,则△ ACD ∽△ CBD∽△ ABC 。例 6. 已知,如图10 所示, D 为△ ABC 内的一点, E 为△ ABC 外的一点,且∠EBC= ∠DBA ,∠ ECB= ∠DAB 。例 7. 已知,如图 11 所示,F为正方形 ABCD 的边 AB 的中点,E 为 AD 上的一点,AE= 41AD ,FG⊥CE 于 G。求证:CGEGFG2。例 8. 已知,如图12 所示,在平行四边形ABCD 中, O 为对角线BD 上的点,过O 作直线分别交 DC 、AB 于 M 、N,交 AD 的延长线于E,交 CB 的延长线于F。求证: OE·ON=OM ·OF。