相似三角形知识在生活中的应用VIP专享

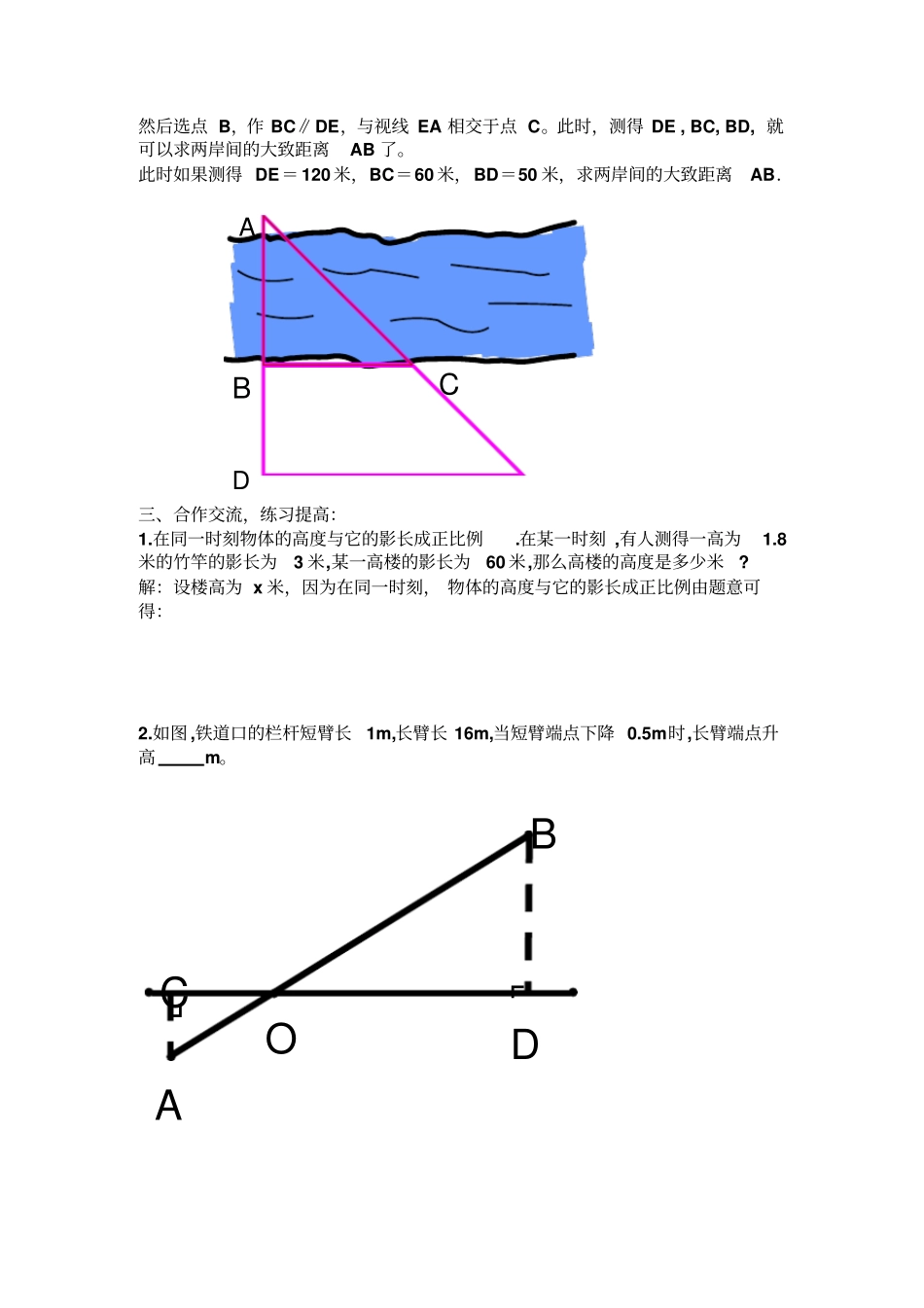
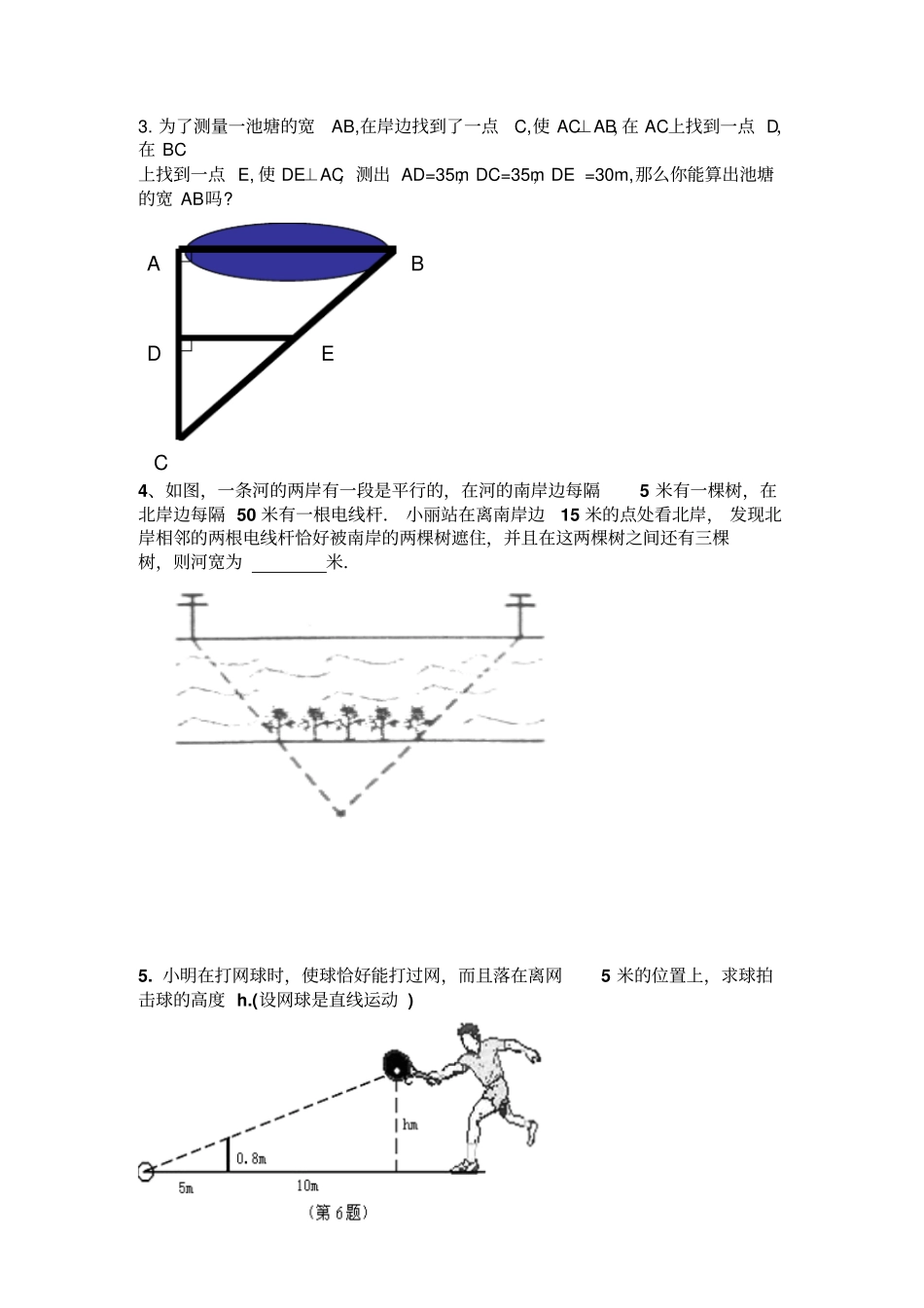
相似三角形的应用学习目标：1、通过练习，让学生 在实际生活中 ,面对不能直接测量物体的高度和宽度时. 可以把它们转化为数学问题,建立相似三角形模型 ,再利用对应边的比相等来达到求解的目的 ! 2. 能掌握并应用一些简单的相似三角形模型. 3．掌握动态三角形的做题方法。一、复习记忆：1、判断两三角形相似有哪些方法? 两角对应相等的两个三角形相似. 三边对应成比例的两个三角形相似. 两边对应成比例 ,且夹角相等的两个三角形相似. 斜边直角边对应成比例的两个三角形相似. 平行于三角形一边的直线截其它两边(或其延长线 ),所截得的三角形与原三角形相似 . 2、相似三角形有什么性对应角相等，对应边的比相二、共同学习，拓展提高：例1：如果 O′ B′ ＝1，A′B′ ＝ 2，AB＝274，求金字塔的高度 OB. 例 2:如图，为了估算河的宽度，我们可以在河对岸选定一个目标作为点A，再在河的这一边选点 B和C，使AB⊥BC，然后，再选点 E，使 EC⊥BC，用视线确定BC和AE的交点 D．此时如果测得 BD＝ 120米，DC＝ 60米， EC＝50米，求两岸间的大致距离 AB．(方法一 )A (方法二 ) 我们在河对岸选定一目标点A，在河的一边选点 D 和 E，使 DE⊥AD，ABBOOAD C E B 然后选点 B，作 BC∥DE，与视线 EA 相交于点 C。此时，测得 DE , BC, BD, 就可以求两岸间的大致距离AB 了。此时如果测得 DE＝ 120 米，BC＝60 米，BD＝50 米，求两岸间的大致距离AB．三、合作交流，练习提高：1.在同一时刻物体的高度与它的影长成正比例.在某一时刻 ,有人测得一高为1.8米的竹竿的影长为3 米,某一高楼的影长为60 米,那么高楼的高度是多少米? 解：设楼高为 x 米，因为在同一时刻， 物体的高度与它的影长成正比例由题意可得：2.如图 ,铁道口的栏杆短臂长1m,长臂长 16m,当短臂端点下降 0.5m时,长臂端点升高m。A D B C O B D C A ┏┛3. 为了测量一池塘的宽AB,在岸边找到了一点C,使 AC⊥AB，在 AC上找到一点 D，在 BC 上找到一点 E, 使 DE⊥AC，测出 AD=35m，DC=35m，DE =30m,那么你能算出池塘的宽 AB吗? 4、如图，一条河的两岸有一段是平行的，在河的南岸边每隔5 米有一棵树，在北岸边每隔 50 米有一根电线杆． 小丽站在离南岸边15 米的点处看北岸， 发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住，并且在这两棵树之间还有三棵树，则河宽为米．5. 小明在打网球时，使球恰好能打过网...