平面向量与三角形三心

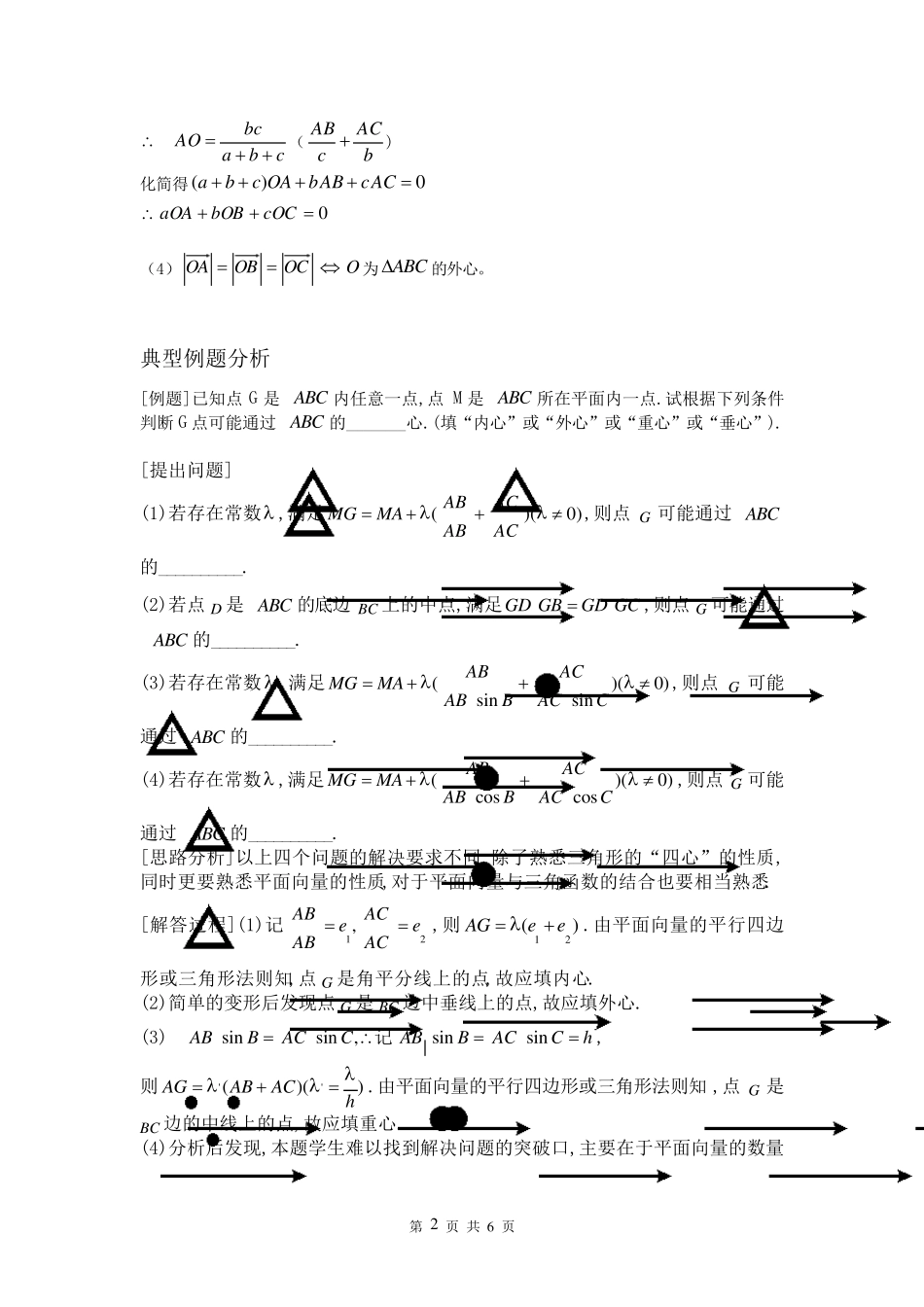
第 1 页 共 6 页 向量与三角形内心、外心、重心、垂心知识的交汇 一、四心的概念介绍 （1）重心——中线的交点：重心将中线长度分成 2：1； （2）垂心——高线的交点：高线与对应边垂直； （3）内心——角平分线的交点（内切圆的圆心）：角平分线上的任意点到角两边的距离相等； （4）外心——中垂线的交点（外接圆的圆心）：外心到三角形各顶点的距离相等。 二、四心与向量的结合 （1）0OCOBOAO 是 ABC的重心. 证法 1：设),(),,(),,(),,(332211yxCyxByxAyxO 0OCOBOA0)()()(0)()()(321321yyyyyyxxxxxx33321321yyyyxxxx  O 是 ABC的重心. 证法 2：如图 OCOBOA 02ODOA ODAO2 DOA、、三点共线，且O 分 AD 为 2：1  O 是 ABC的重心 （2）OAOCOCOBOBOAO 为 ABC的垂心. 证明：如图所示 O 是三角形ABC 的垂心，BE 垂直 AC，AD 垂直 BC， D、E 是垂足. 0)(CAOBOCOAOBOCOBOBOA ACOB  同理BCOA ，ABOC   O 为 ABC的垂心 （3）设 a ,b ,c 是三角形的三条边长，O 是 ABC 的内心 OOCcOBbOAa0为 ABC的内心. 证明：bACcAB、分别为ACAB、方向上的单位向量， bACcAB 平分BAC, ( AObACcAB )，令cbabc OABCDEOABCDE 第 2 页 共 6 页 cbabcAO（ bACcAB ) 化简得0)(ACcABbOAcba 0OCcOBbOAa （4）OCOBOA O 为ABC的外心。 典型例题分析 [例题]已知点G 是ABC 内任意一点,点 M 是ABC 所在平面内一点.试根据下列条件判断G 点可能通过ABC 的_______心.(填“内心”或“外心”或“重心”或“垂心”). [提出问题] (1)若存在常数 ,满足()(0)ABACMGMAABAC,则点G 可能通过ABC的__________. (2)若点D 是ABC 的底边 BC 上的中点,满足GD GBGD GC,则点G 可能通过ABC 的__________. (3)若存在常数 ,满足()(0)sinsinABACMGMAABBACC,则点G 可能通过ABC 的__________. (4)若存在常数 ,满足()(0)coscosABACMGMAABBACC,则点G 可能通过ABC 的__________. [思路分析]以上四个问题的解决要求不同,除了熟悉三角形的“四心”的性质,同时更要熟悉平面向量的性质,对于平面向量与三角函数的结...