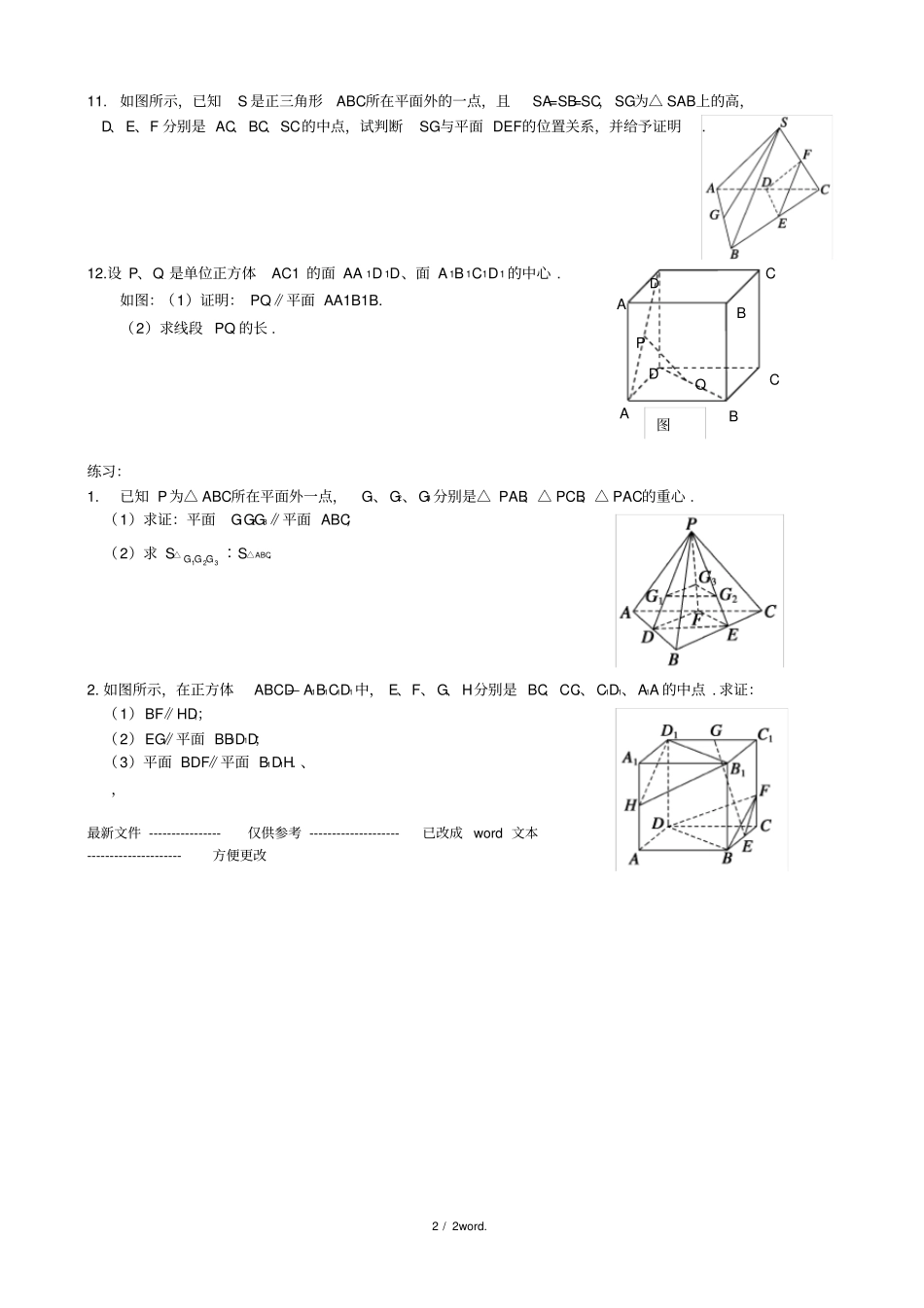
1 / 2word. 空间中的平行关系直线与平面平行的判定定理:平面与平面平行的判定定理:直线与平面平行的性质定理:平面与平面平行的性质定理:1.以下说法中正确的个数是(其中a, b 表示直线,表示平面)( ) ①若 a∥b, b∥,则 a∥②若 a∥,b∥,则 a∥b ③若 a∥b, b,则 a∥④若 a∥,b∥,则 a 与 b 相交A. 0 个B. 1 个C. 2 个D. 3 个2.a∥, b∥,a∥b,则与的位置关系是()A.平行B.相交C.平行或相交D.一定垂直3.如果平面外有两点 A 、B,它们到平面的距离都是d,则直线 AB 和平面的位置关系一定是()A. 平行B.相交C.平行或相交D. AB4.当∥ 时,必须满足的条件()A. 平面内有无数条直线平行于平面B.平面与平面同平行于一条直线C.平面内有两条直线平行于平面D.平面内有两条相交直线与平面平行5.直线 a∥平面,点 A∈,则过点 A 且平行于直线a 的直线()A. 只有一条,但不一定在平面内B.只有一条,且在平面内C.有无数条,但都不在平面内D.有无数条,且都在平面内6. A、B 是直线 l 外的两点,过A、B 且和 l 平行的平面的个数是()A.0 个B.1 个C.无数个D.以上都有可能7.设, 是不重合的两个平面,l 和 m 是不重合的两条直线,则能得出∥ 的是()A. l,m,且 l∥ ,m∥B. l, m,且 l∥mC. l,l∥ m,且 m∥D.l∥,m∥ ,且 l∥m 8. 如图所示,在三棱柱ABC— A1B1C1 中, M、N分别是 BC和 A1B1的中点 . 求证: MN∥平面 AA1C19.正方体 AC 1 中, E、 F、G 分别为 B 1C1、A 1D 1、A 1B 1 的中点求证:平面EBD// 平面 FGA .10、已知 E、F、G、H为空间四边形ABCD的边 AB、BC、CD、DA上的点,且 EH∥FG.求证: EH∥BD. HGFEDBAC2 / 2word. BP 图DACD ABCQ 11. 如图所示,已知S 是正三角形ABC所在平面外的一点,且SA=SB=SC,SG为△ SAB上的高,D、E、F 分别是 AC、BC、SC的中点,试判断SG与平面 DEF的位置关系,并给予证明. 12.设 P、Q 是单位正方体AC1 的面 AA 1D 1D、面 A 1B 1C1D1 的中心 . 如图:(1)证明: PQ∥平面 AA1B1B. (2)求线段 PQ 的长 . 练习:1.已知 P为△ ABC所在平面外一点,G1、G2、G3 分别是△ PAB、△ PCB、△ PAC的重心 . (1)求证:平面G1G2G3∥平面 ABC;(2)求 S△321GGG∶S△ABC. 2. 如图所示,在正方体ABCD— A1B1C1D1中, E、F、G、H分别是 BC、CC1、C1D1、A1A 的中点 . 求证:(1)BF∥HD1;(2)EG∥平面 BB1D1D;(3)平面 BDF∥平面 B1D1H. 、,最新文件 ---------------- 仅供参考 --------------------已改成 word 文本--------------------- 方便更改