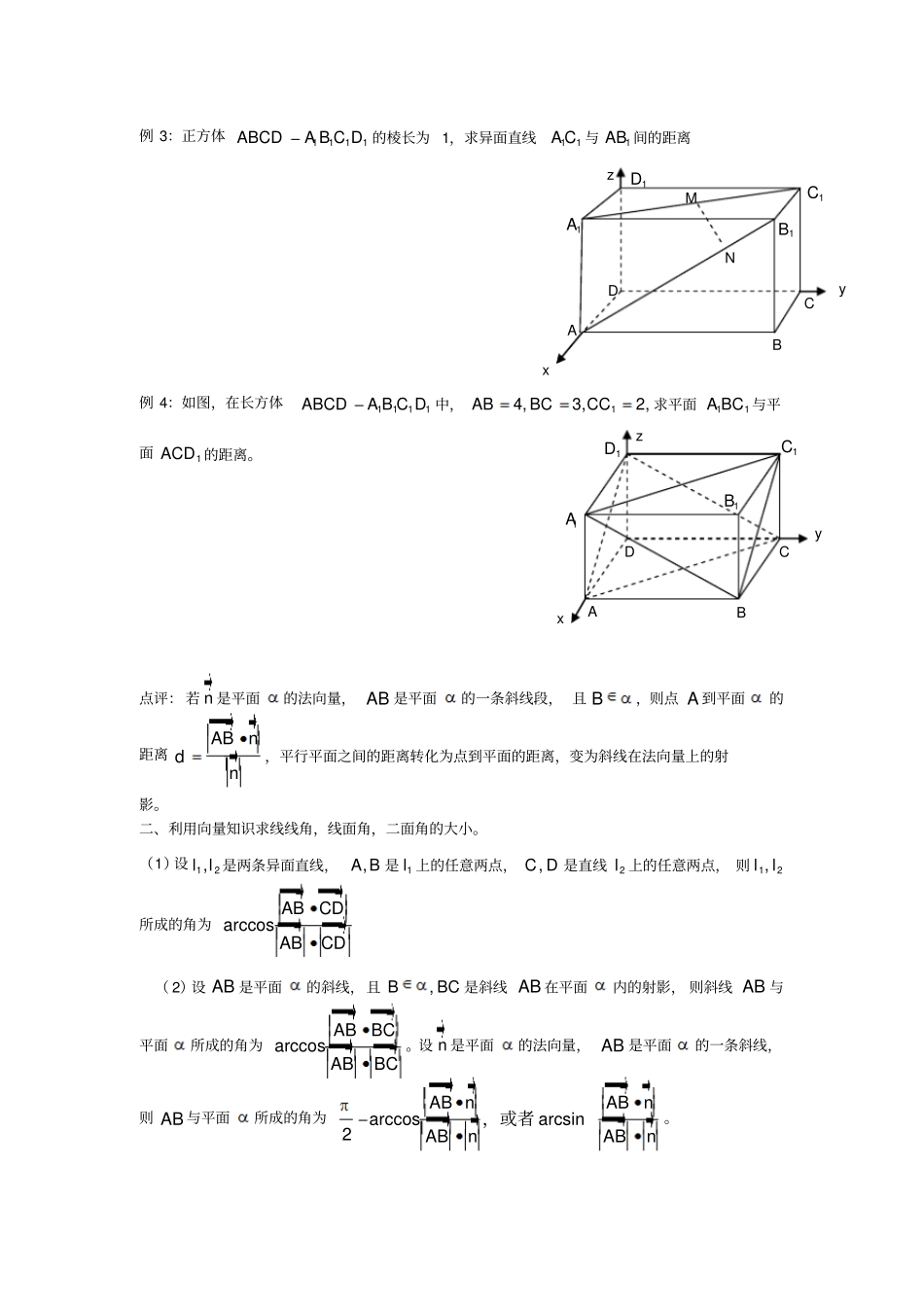
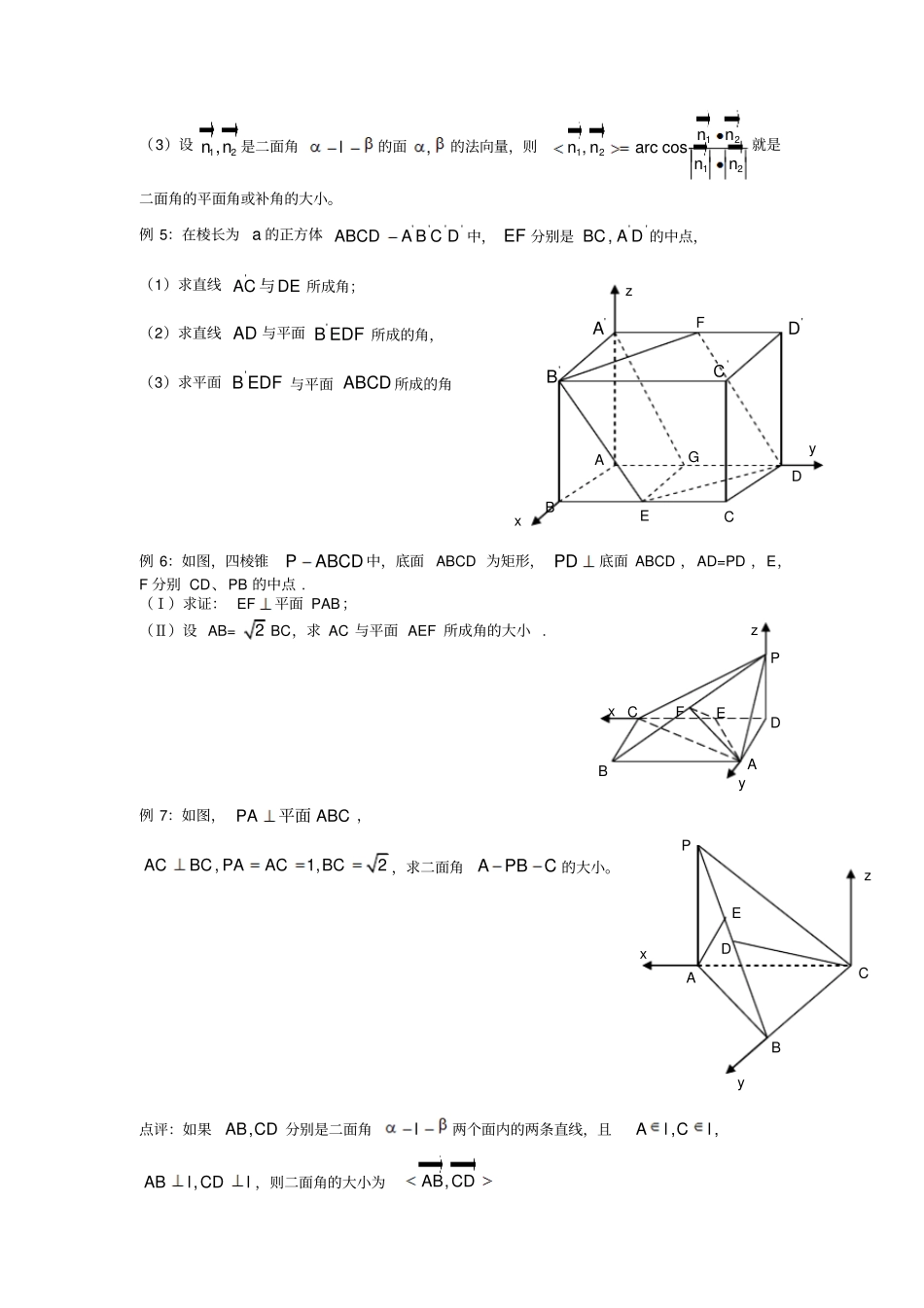
立体几何中几类典型问题的向量解法空间向量的引入为求立体几何的空间角和距离问题、证线面平行与垂直以及解决立体几何的探索性试题提供了简便、快速的解法。 它的实用性是其它方法无法比拟的,因此应加强运用向量方法解决几何问题的意识,提高使用向量的熟练程度和自觉性,注意培养向量的代数运算推理能力,掌握向量的基本知识和技能,充分利用向量知识解决图形中的角和距离、平行与垂直问题。一、利用向量知识求点到点,点到线,点到面,线到线,线到面,面到面的距离(1)求点到平面的距离除了根据定义和等积变换外还可运用平面的法向量求得,方法是:求出平面的一个法向量的坐标,再求出已知点P 与平面内任一点M 构成的向量MP 的坐标,那么 P 到平面的距离cos,n MPdMPn MPn(2)求两点,P Q 之间距离,可转化求向量PQ 的模。(3)求点 P 到直线 AB 的距离,可在AB 上取一点 Q ,令,AQQB PQAB 或 PQ的最小值求得参数,以确定 Q 的位置,则 PQ 为点 P 到直线 AB 的距离。还可以在 AB 上任取一点 Q 先求ABPQ,cos,再转化为ABPQ,sin,则 PQABPQ,sin为点 P 到直线 AB 的距离。(4)求两条异面直线12,l l 之间距离,可设与公垂线段AB 平行的向量 n ,,C D 分别是12,ll 上的任意两点,则12,ll 之间距离CDnABn例 1:设(2,3,1),(4,1,2),(6,3,7),( 5, 4,8)ABCD,求点 D 到平面 ABC 的距离例 2:如图,正方形ABCD、 ABEF 的边长都是1,而且平面 ABCD 、 ABEF 互相垂直。点 M 在 AC 上移动,点 N 在 BF 上移动,若aBNCM)20(a。(Ⅰ)求 MN 的长;(Ⅱ)当 a 为何值时, MN 的长最小;(Ⅲ)当 MN 长最小时,求面MNA 与面 MNB 所成的二面角的大小A(O) B D C x E F N M y z 例 3:正方体1111ABCDA B C D 的棱长为 1,求异面直线11A C 与1AB 间的距离例 4:如图,在长方体1111ABCDA B C D 中,14,3,2,ABBCCC求平面11A BC 与平面1ACD 的距离。点评: 若 n 是平面的法向量, AB 是平面的一条斜线段, 且 B,则点 A 到平面的距离ABndn,平行平面之间的距离转化为点到平面的距离,变为斜线在法向量上的射影。二、利用向量知识求线线角,线面角,二面角的大小。(1)设 12,l l 是两条异面直线,,A B 是 1l 上的任意两点,,C D 是直线2l 上的任意两点, 则12,ll所成的角为 arccosABCDABCD( 2)设 AB 是平面的斜线,且,BBC 是斜...