立体几何动态问题翻折问题

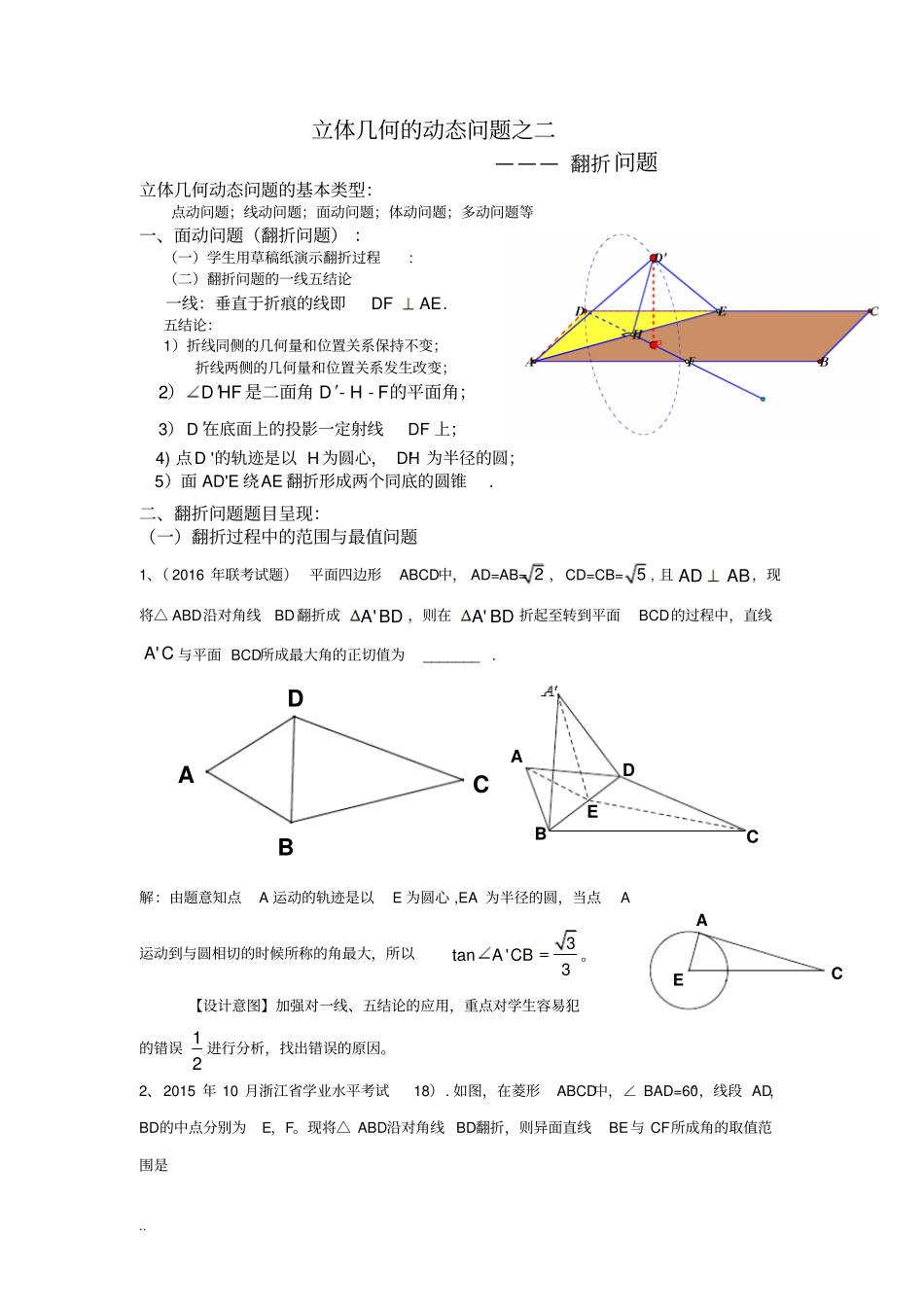
.. 立体几何的动态问题之二——— 翻折问题立体几何动态问题的基本类型：点动问题；线动问题；面动问题；体动问题；多动问题等一、面动问题（翻折问题） ：（一）学生用草稿纸演示翻折过程: （二）翻折问题的一线五结论.DFAE一线：垂直于折痕的线即五结论：1）折线同侧的几何量和位置关系保持不变；折线两侧的几何量和位置关系发生改变；2--D HFDHF）是二面角的平面角；3DDF）在底面上的投影一定射线上；二、翻折问题题目呈现：（一）翻折过程中的范围与最值问题1、（ 2016 年联考试题） 平面四边形ABCD中， AD=AB= 2 ，CD=CB= 5 , 且 ADAB，现将△ ABD沿对角线BD翻折成'A BD ，则在'A BD 折起至转到平面BCD的过程中，直线'A C 与平面 BCD所成最大角的正切值为_______ . 解：由题意知点A 运动的轨迹是以E 为圆心 ,EA 为半径的圆，当点A运动到与圆相切的时候所称的角最大，所以3tan'3A CB。【设计意图】加强对一线、五结论的应用，重点对学生容易犯的错误 12进行分析，找出错误的原因。2、2015 年 10 月浙江省学业水平考试18）. 如图，在菱形ABCD中，∠ BAD=60°，线段 AD，BD的中点分别为E，F。现将△ ABD沿对角线 BD翻折，则异面直线BE与 CF所成角的取值范围是DABECDABC4) ''DHDH点的轨迹是以为圆心，为半径的圆；5AD'EAE.）面绕翻折形成两个同底的圆锥ECA.. A. (,)6 3B. (,]62C. (,]32D. 2(,)33分析：这是一道非常经典的学考试题，本题的解法非常多，很好的考查了空间立体几何线线角的求法。方法一 ：特殊值法（可过F 作 FH平行 BE,找两个极端情形）方法二 ：定义法：利用余弦定理：222254cos243FHFCCHFHCCHFH FC，有 32144CH1 1cos,2 2CFH异面直线 BE与 CF所成角的取值范围是(,]3 2方法三：向量基底法：111()()222BE FCBABDFCBA FCBFFA FC11 1cos,cos,,22 2BE FCFC FA方法四：建系：3、（ 2015 年浙江· 理8）如图，已知ABC， D 是 AB 的中点，沿直线CD 将ACD 折成A CD ，所成二面角ACDB 的平面角为，则（ B ）A. A DB B. A DBC. A CB D. A CB方法一 ：特殊值方法二 ：定义法作出二面角，在进行比较。方法三 ：抓住问题的本质，借助圆锥利用几何解题。4、（14 年 1 月浙江省学业学考试题）如图在 Rt△ABC中，AC＝1，BC＝ x，D是斜边 AB的中点，将 △BCD沿直线 CD翻折，若在翻折过程中存在某EFBDCAH.. 个位置，使得CB⊥AD，则 x 的取...