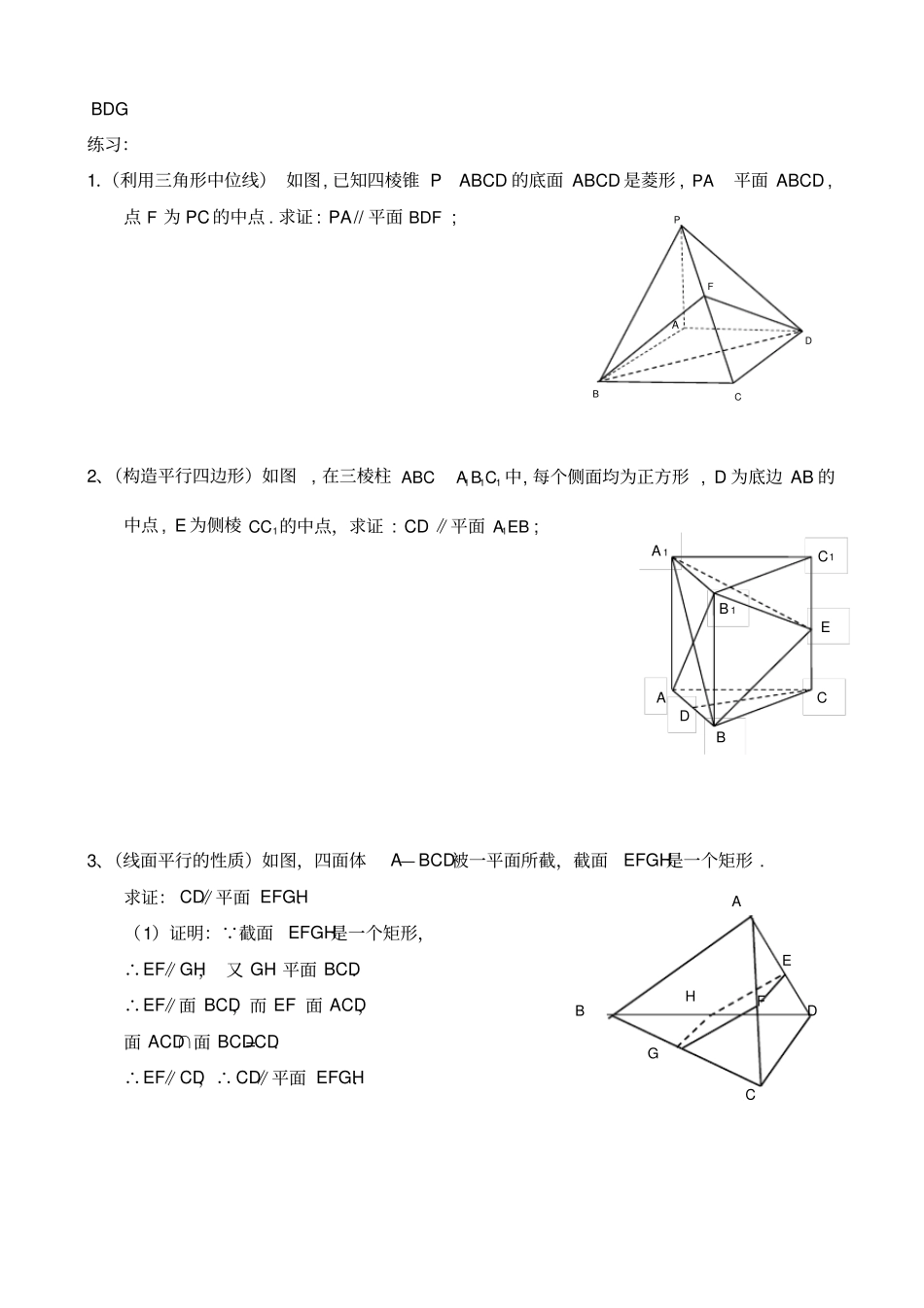
立体几何专题――平行1、若直线 l 不平行于平面 a , 且 la , 则 B (A) a 内所有直线与 l 异面 (B) a 内不存在与 l 平行的直线(C) a 内存在唯一的直线与 l 平行 (D) a 内的直线与 l 都相交2、一条直线若同时平行于两个相交平面, 那么这条直线与这两个平面的交线的位置关系是( C ) A.异面 B.相交 C.平行 D.不能确定3、一个正方体的所有顶点都在同一球面上, 若球的体积是 4 π3, 则正方体的表面积是 A(A)8 (B)6 (C)4 (D)3 4、在正三棱柱ABC— A1B1C1中,AA1=AB,则 AC1 与平面 BB1C1C 所成的角的正弦值为 ( C )A.22B.515 C.46D.365、某四棱锥的三视图如图所示, 该四棱锥的表面积是B (A)32 (B) 16162(C)48 (D) 163221、线线平行的判断:(1)三角形中位线定理;(2)构造平行四边形,其对边平行;(3)对应线段成比例,两直线平行;(4)平行于同一直线的两直线平行; (平行的传递性)(5)如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行;(线面平行的性质)(6)如果两个平行平面同时和第三个平面相交,所得交线平行;(面面平行的性质)(7)垂直于同一平面的两直线平行; (线面垂直的性质)2、线面平行的判断:(1)如果平面外的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行。(2)两个平面平行,其中一个平面内的直线必平行于另一个平面。侧(左)视图俯视图4 4 正 (主 )视图2 例 1、(三角形中位线定理) 如图,在正方体1111ABCDA B C D 中,E 是1AA 的中点,求证:1//A C平面 BDE 。证明:连接 AC 交 BD 于 O,连接 EO , E 为1AA 的中点, O 为 AC 的中点∴ EO 为三角形1A AC 的中位线∴1//EOAC又 EO 在平面 BDE 内,1A C 在平面 BDE 外∴1//A C平面 BDE 。例 2、(证明是平行四边形)已知正方体1111ABCDA B C D ,O 是底 ABCD 对角线的交点 .求证:C1O∥面11AB D ;证明:(1)连结11A C ,设11111A CB DO ,连结1AO 1111ABCDA B C D 是正方体11A ACC 是平行四边形∴A1C1∥AC 且11A CAC又1,O O 分别是11,A CAC 的中点,∴ O1C1∥AO 且11O CAO11AOC O 是平行四边形111,C OAOAO∥面11AB D ,1C O面11AB D ∴C1O∥面11AB D3、面面平行的判断:(1)一个平面内的两条相交直线分别平行于另一个平面,这两个平面平行。(2)垂直于...