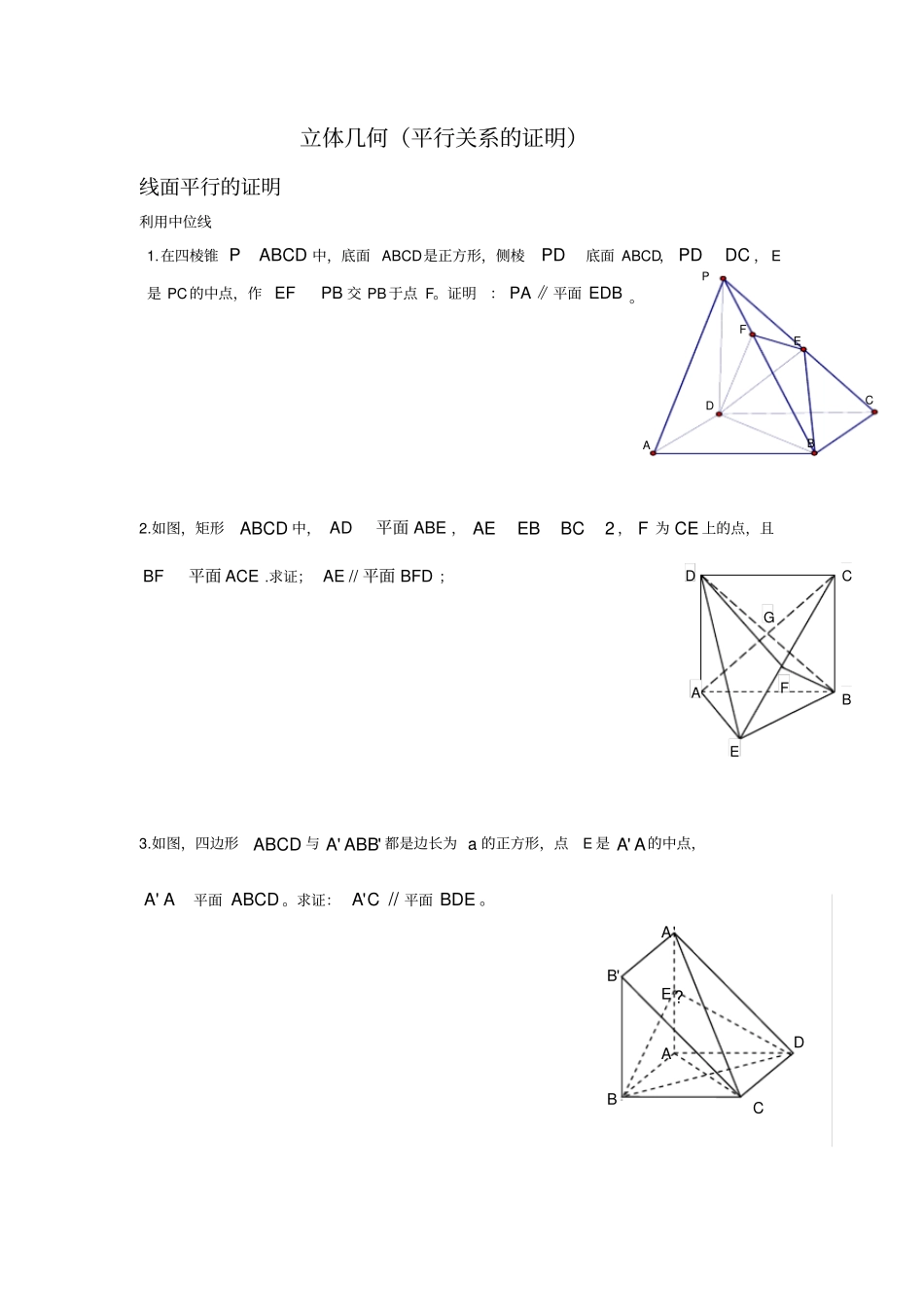
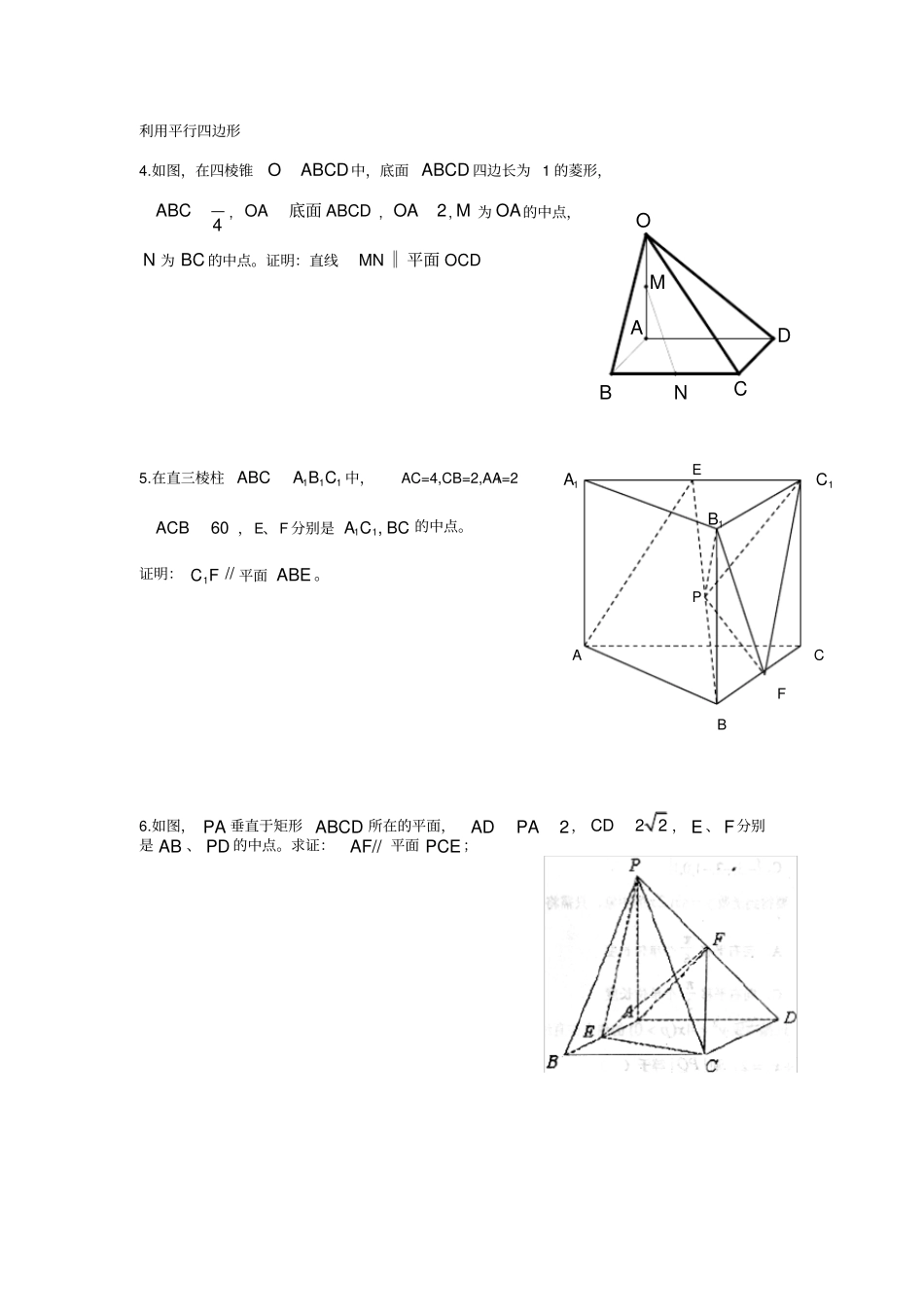
ABCDPEF立体几何(平行关系的证明)线面平行的证明利用中位线1.在四棱锥ABCDP中,底面 ABCD是正方形,侧棱PD底面 ABCD,DCPD, E是 PC的中点,作PBEF交 PB于点 F。证明:∥PA平面 EDB 。2.如图,矩形ABCD 中,ABEAD平面,2BCEBAE, F 为 CE 上的点,且ACEBF平面.求证;BFDAE平面//;3.如图,四边形ABCD 与'' ABBA都是边长为 a 的正方形,点E 是AA'的中点,'A A平面 ABCD 。求证:CA'// 平面 BDE 。ABCDEFGB'?D C A'B A E NMABDCOA B C E F P 1A1C1B利用平行四边形4.如图,在四棱锥OABCD中,底面 ABCD 四边长为 1 的菱形,4ABC, OAABCD底面, 2OA, M 为 OA的中点,N 为 BC 的中点。证明:直线MNOCD平面‖5.在直三棱柱111CBAABC中,AC=4,CB=2,AA1=260ACB,E、F 分别是BCCA,11的中点。证明://1FC平面 ABE 。6.如图, PA 垂直于矩形 ABCD 所在的平面,ADPA2, CD22 , E 、 F分别是 AB 、 PD 的中点。求证:AF// 平面 PCE;BACDEMNP利用比例7.如下图,设 P 为长方形 ABCD所在平面外一点, M,N 分别为 AB,PD上的点,且MBAM=NPDN ,求证:直线MN ∥平面 PBC.8.如图,正方形 ABCD 的边长为 13,平面 ABCD 外一点 P 到正方形各顶点的距离都是13,M , N 分别是 PA , DB 上的点,且5 8PMMABN ND∶∶∶ .求证:直线MN //平面 PBC 。9 正方形 ABCD交正方形 ABEF于 AB(如图所示) M、N 在对角线 AC、 FB上且 AM= FN。求证: MN 图,在四棱锥V-ABCD中,底面 ABCD是矩形,侧棱VA⊥底面 ABCD,E、F、G 分别为 VA、 VB、BC 的中点.求证:平面EFG∥平面 VCD。11.在四棱锥ABCDP中, ABCD 是矩形,NME、、分别是PCABCD、、的中点 .证明:平面//EMN平面 PAD .ABCENDMPD A B C F E M N ACDBBADCFEFEG12.在直角梯形 ABCD 中,BCAD //,2222ABADBC,90ABC,且 E 、F 分别为 AB 、 AD 的点,如图1,把ABD 沿 BD 对折,使得平面ABD 与平面 BCD 不重合 .在图 2 中,若ACAGADAFABAE,求证:平面//EFG平面 BCD .