组合变形习题解答

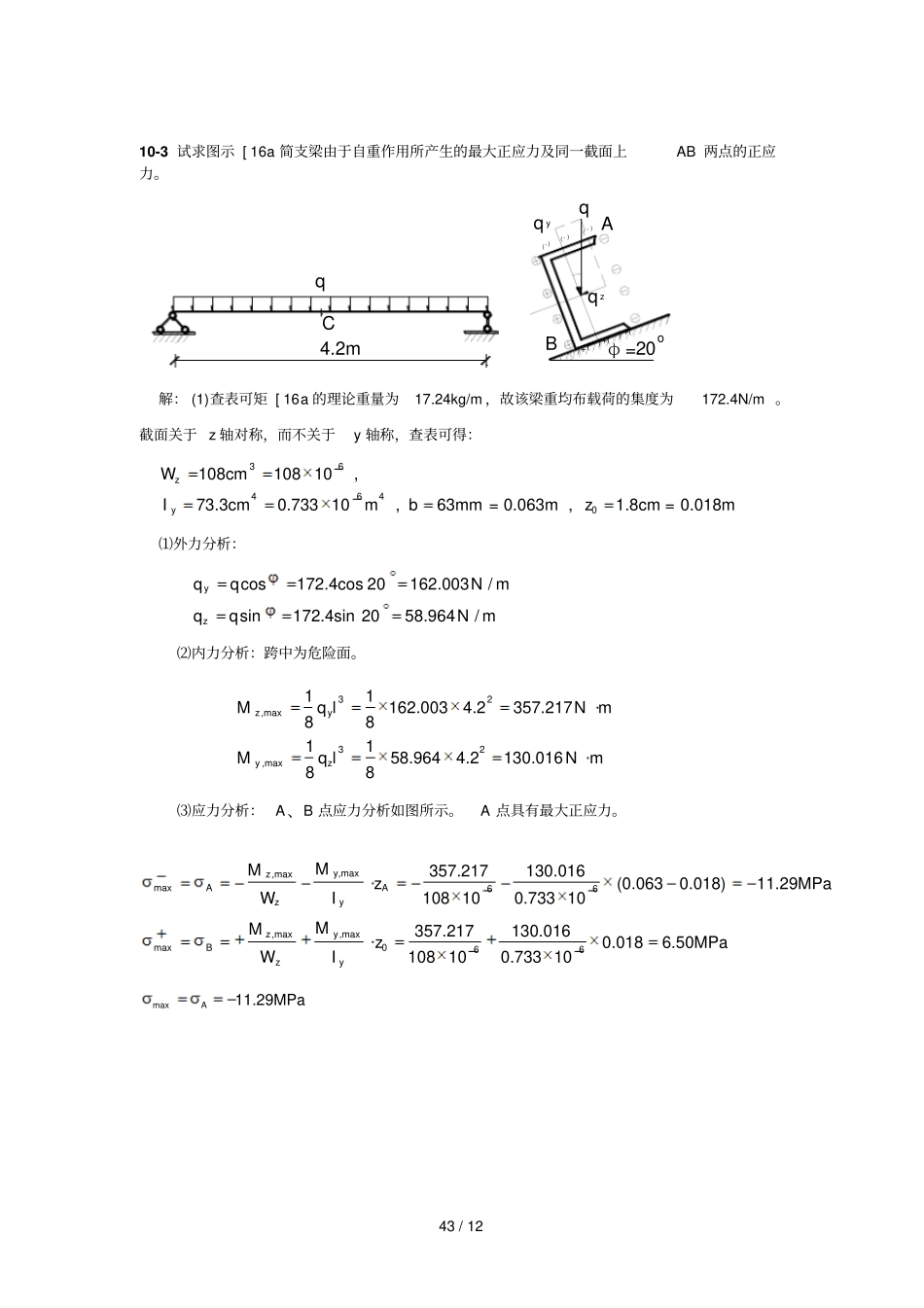
43 / 12 10-3 试求图示 [ 16a 简支梁由于自重作用所产生的最大正应力及同一截面上AB 两点的正应力。( - )( - )( - )qq y4.2mCφo=20(+)(+)(+)qq zAB解： (1)查表可矩 [ 16a 的理论重量为17.24kg/m ，故该梁重均布载荷的集度为172.4N/m 。截面关于 z 轴对称，而不关于y 轴称，查表可得：364640108cm10810,73.3cm0.733 10m,63mm = 0.063m ,1.8cm = 0.018mzyWIbz⑴外力分析：cos172.4cos 20162.003/sin172.4sin 2058.964/yzqqNmqqNm⑵内力分析：跨中为危险面。32,max32,max11162.0034.2357.217881158.9644.2130.01688zyyzMq lN mMq lN m⑶应力分析： A、B 点应力分析如图所示。A 点具有最大正应力。,max,maxmax66,max,maxmax066357.217130.016(0.0630.018)11.29MPa108 100.733 10357.217130.0160.0186.50MPa108100.733 10yzAAzyyzBzyMMzWIMMzWImax11.29MPaA44 / 12 10-4 试求图示简支梁的最大正应力，及跨中的总挠度。已知弹性模量100PaEG。解： (1) 外力分析：由于集中力在横截面内与轴线垂直，故梁将发生斜弯曲。cos10cos159.66kNsin10sin152.59kNyzPPPP⑵内力分析：集中力作用在跨中，故跨中横截面为危险面。,max,max119.6637.245kNm44112.5931.943kNm44zyyzMP lMP l⑶应力分析：跨中横截面D 2、D 1 点分别具有最大的拉压应力，应力分析如图所示。133,max,maxmax227.245 101.943 10(Pa)110.150.200.200.15667.2452.591(MPa)9.836MPayzDzyMMWW2,max,maxmax7.2452.591(MPa)9.836MPayzDzyMMWW（4）求梁的跨中的总挠度。45 / 12 9.66kNyP使简支梁上下弯曲，发生挠度f y;2.59kNzP使简支梁前后弯曲，发生挠度 f z。查《教材》 P.156第 12 栏，可知跨中的挠度333-439333-4399.66 10310 m=0.5434mm480.150.2048 (100 10 )122.59 1032.59 10 m = 0.259mm480.200.1548(100 10 )12yyzzzyP lfEIP lfEI故：2222-45.4342.59 10 m0.602mm5.434tan2.09864.522.59zyzyfffff10-5 由 木 材 制 成 的 矩 形 截 面 悬 臂 梁 受 力 、 尺 寸 如 图 所 示 。 材 料 的 弹 性 模 量41. 01 0 M P aE。试：（1）求梁的最大正应力及其作用点的位置；（ 2）求梁的最大挠度。（3）如果截面是圆形，130mmd，试求梁横截面的最大正应力。2my1mD 2D 1zx+ + +180(-)(-)(-)(-)D290(+)(+)(+)(+)D 1 - - - yzP2=0.8kNP 1=1.6kNMyx(N m)(N m)3200xP2M...