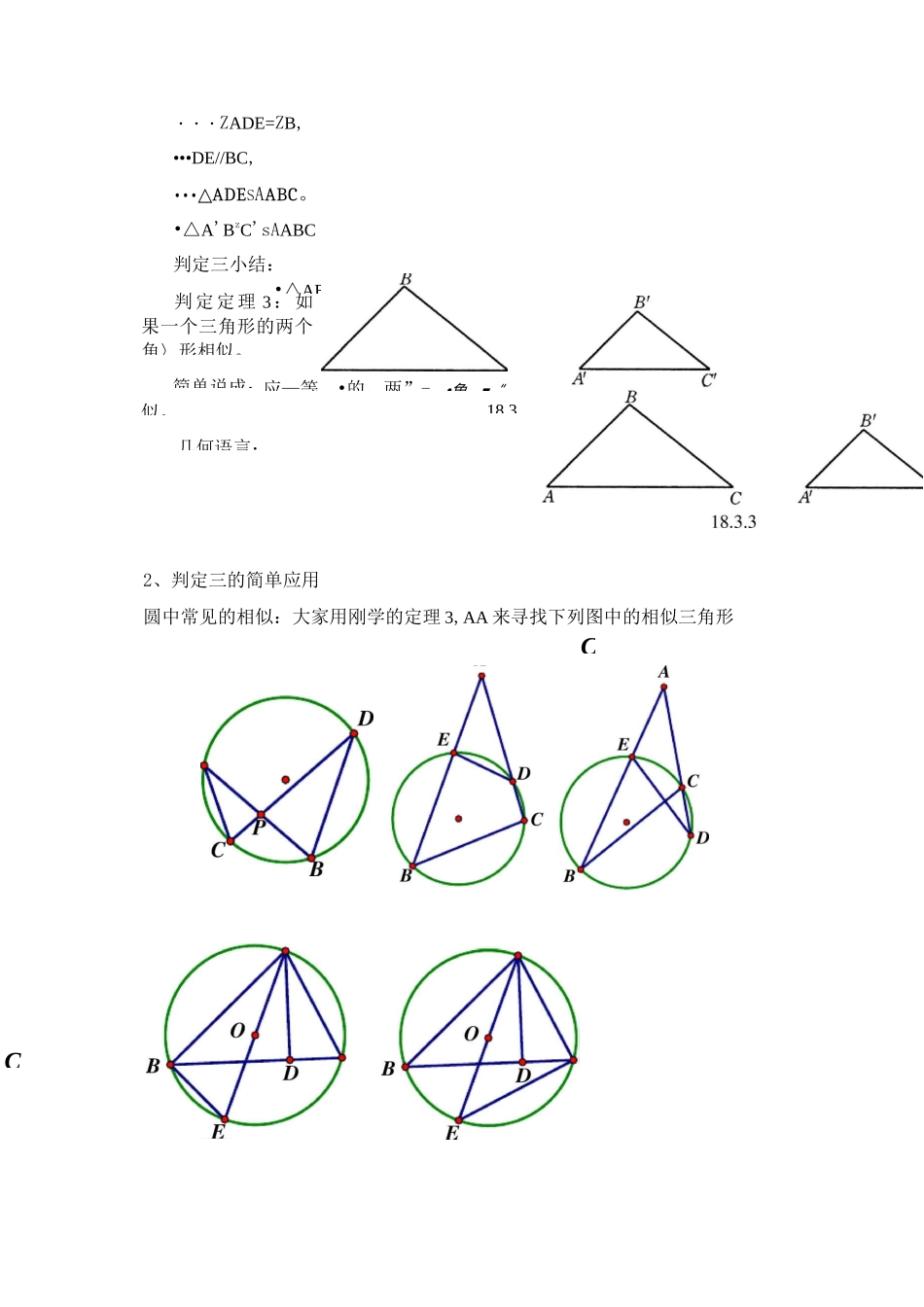
相似三角形的判定(三)福清三山中学:游书兵一、教学目标1.经历两个三角形相似的探索过程,体验分析归纳得出数学结论的过程,进一步发展学生的探究、交流能力.2.掌握三角形相似的判定条件(AA)。3.会运用“两个角对应相等的三角形相似”判断常见图形中的三角形相似,并应用判定三解决简单的问题.二、教学重点1.相似三角形的判定三的应用。与三角形相似的预备定理及平行线平分线段成比例定理和推论.2.认识直角三角形斜边上的高所分的两个三角形与原三角形相似三、教学难点1.相似三角形的判定三的证明。2.相似三角形的判定三的应用.3.难点的突破方法(1)对于判定三的证明,参考判定一和判定二的证明思路,把较小的三角形移到另一个三角形的内的思路,即利用已有条件构造全等三角形。(2)利用圆中的相似三角形和直角三角形斜边上的高构成的相似三角形的展示,让学生形成应用判定三的意识,即:如果两个三角形具有公共角或对顶角,或两个三角形是直角三角形,那么只要再有一个角对应相等就会相似。四、教学过程一)、引入我们学习了哪几种判定三角形相似的方法?1、定义2、预备定理(由平行得到相似)3、相似三角形的判定一4、相似三角形的判定二探究:如图:AABC 和厶 ABzC,当它们具备什么样的条件时,能够判定它们相似?BcBTC(通过探究,进一步巩固判定一、二)判定三的引入:对比思考观察下表中全等三角形和相似三角形的判定方法,对比之后进行思考:全等三角形中的 ASA 和 AAS 应该对应相似中的什么方法呢?定义判定方法全等三角形三角,三边对应相等的三角形全等。边边边(SSS)边角边CSAS)角边角(ASA)角角边(AAS)和似二角形三角对应相等,三边対应成比例的三角形相似。三边对应成比例(SSS)两边对应成比例且夹角相等(SAS)777***在学生猜想出 AA 后提出问题:在刚才的探究问题中,如果△ABC 和厶 ABC'中,ZA=ZA‘,ZB=ZB.问△ABC 与厶 ABzC 是否相似?(二)、新课讲解1、判定三的证明猜想:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。如图,已知:在厶 ABC 和 AA'BzC 中,ZA=ZAz,ZB=BZ。求证:△ABCS^A'B'C分析:把小的三角形移动到大的三角形上。如何移动呢?证明:在 AABC 的边 AB、AC 上,分别截取 AD=A'B',AE=A'C',连结 DE。•/AD=A'B',ZA=ZA',AE=A'C'・•・△ADE 竺 AA'B'C'・・・ZADE 二ZB',又 TZB'二ZB,似。简单说成:18.3.几何语言:•△ABCsAA'B'C'・・・ZADE=...