弹性力学简明教程(第四版)_习题解答

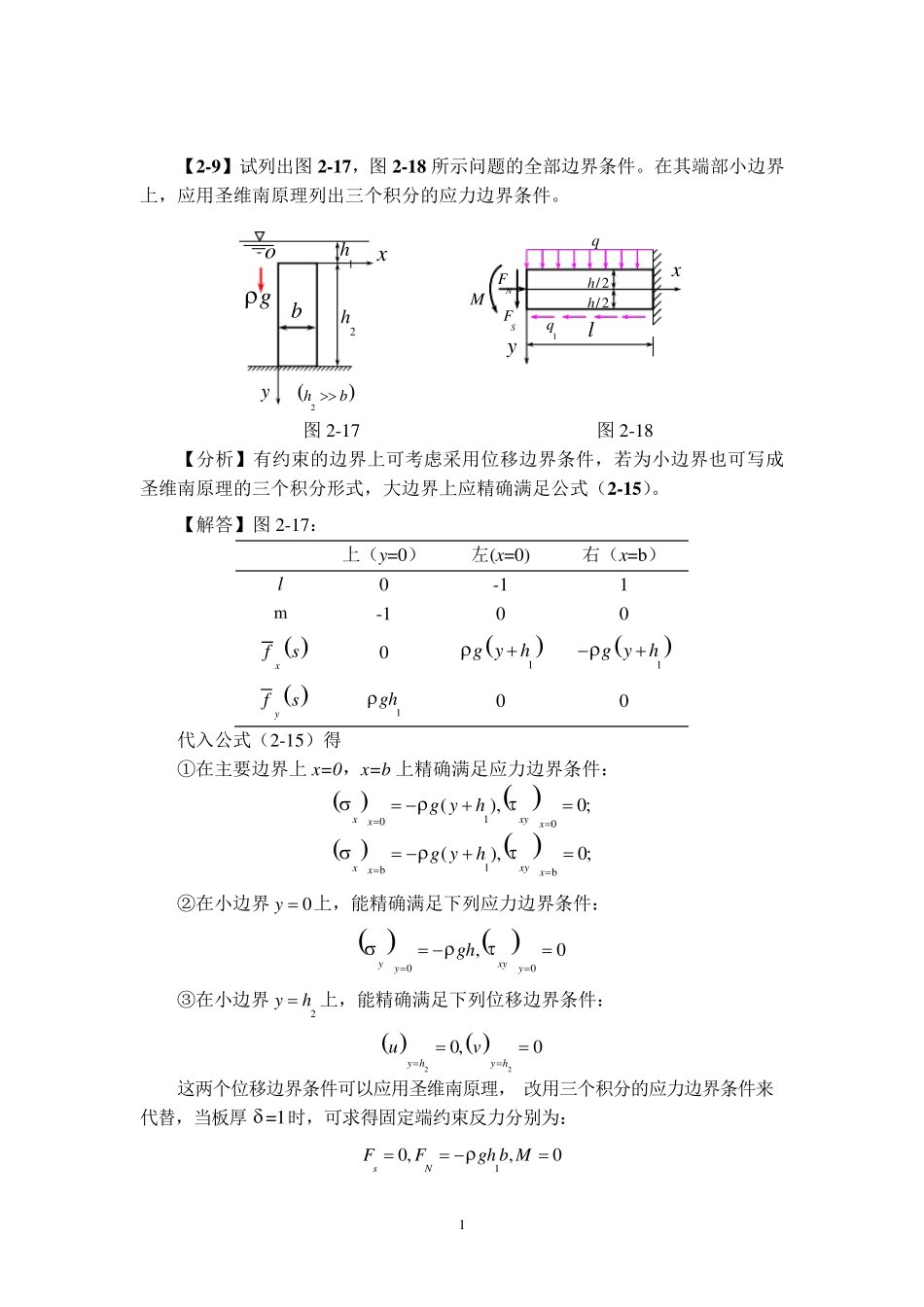
1 【2 -9 】试列出图2 -1 7 ，图2 -1 8 所示问题的全部边界条件。在其端部小边界上，应用圣维南原理列出三个积分的应力边界条件。 xy2h1hbgo2hb hxyl/2/2hMNFSF1qq 图2-17 图2-18 【分析】有约束的边界上可考虑采用位移边界条件，若为小边界也可写成圣维南原理的三个积分形式，大边界上应精确满足公式（2 -1 5 ）。 【解答】图2-17： 上（y=0） 左(x=0) 右（x=b） l 0 -1 1 m -1 0 0   xfs 0 1g yh 1g yh   yfs 1gh 0 0 代入公式（2-15）得 ①在主要边界上x=0，x=b 上精确满足应力边界条件：  100(),0; xxyxxg yh  1bb(),0; xxyxxg yh ②在小边界0y 上，能精确满足下列应力边界条件：   00,0yxyyygh  ③在小边界2yh上，能精确满足下列位移边界条件：   220,0y hy huv 这两个位移边界条件可以应用圣维南原理，改用三个积分的应力边界条件来代替，当板厚=1时，可求得固定端约束反力分别为： 10,,0sNFFgh b M  2 由于2yh为正面，故应力分量与面力分量同号，则有：    222100000byy hbyy hbxyy hdxgh bxdxdx  ⑵图2-18 ①上下主要边界 y=-h/2，y=h/2 上，应精确满足公式（2-15） l m xf (s) yf (s) 2hy   0 -1 0 q 2hy  0 1 -1q 0 - / 2()yyhq ，- / 2()0yxyh，/ 2()0yy h，/ 21()yxy hq  ②在 x =0 的小边界上，应用圣维南原理，列出三个积分的应力边界条件：负面上应力与面力符号相反，有 / 20/ 2/ 20/ 2/ 20/ 2()()()hxyxShhxxNhhxxhdxFdxFydxM    ③在 x=l 的小边界上，可应用位移边界条件0,0lxlxvu这两个位移边界条件也可改用三个积分的应力边界条件来代替。 首先，求固定端约束反力，按面力正方向假设画反力，如图所示，列平衡方程求反力： 110,xNNNNFFFq lFq lF 0,0ySSSSFFFqlFqlF  2211110,'02222ASSq lhqlMMMF lqlq lhMMF l 由于x=l 为正面，应力分量与面力分量同号，故 MNFSF 3 / 21/...