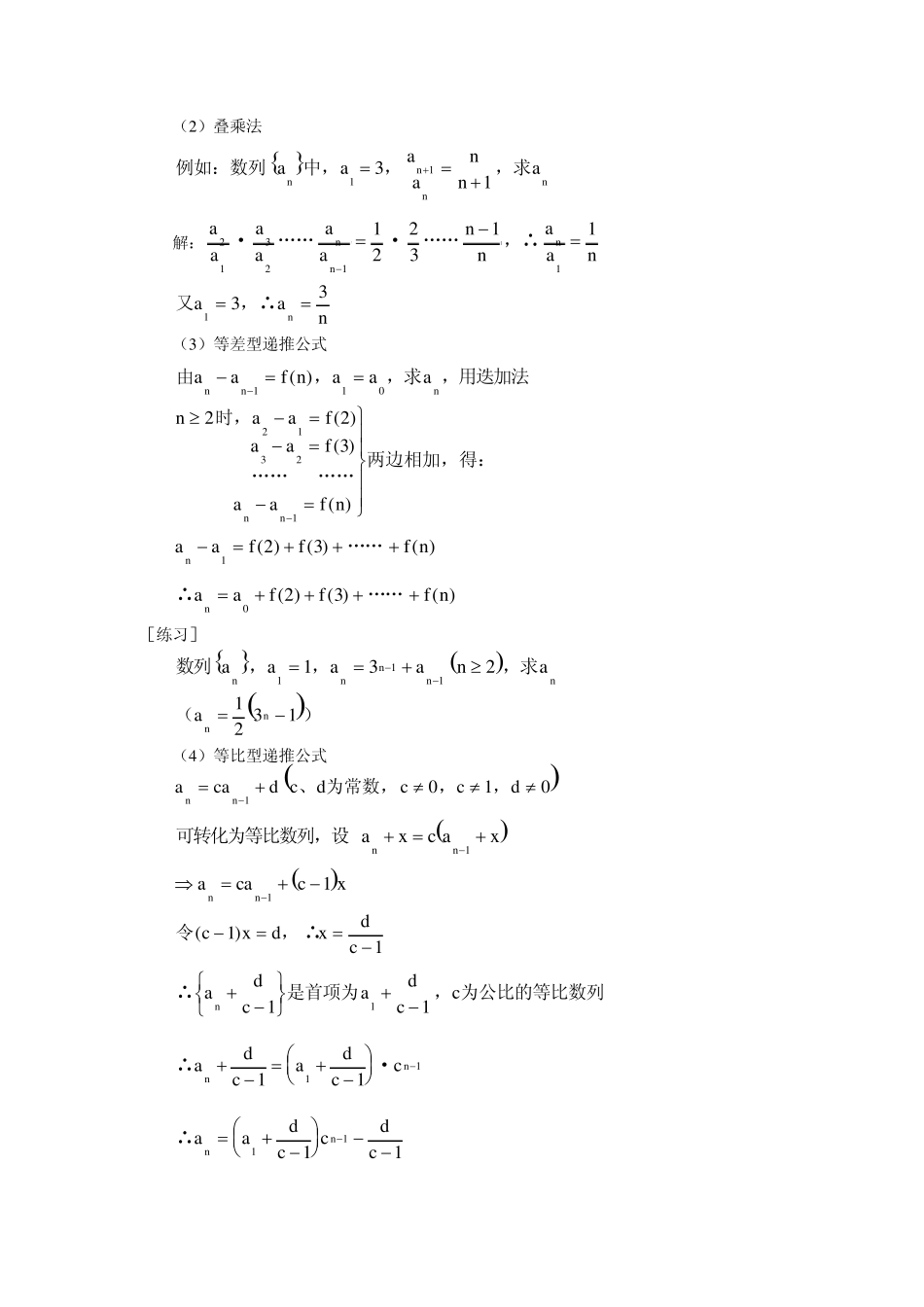数列、排列组合、二项式定理、概率统计知识点总结

数列及排列组合二项式定理知识点总结 1. 等比数列的定义与性质 定义： （为常数，），aaq qqaa qnnnn1110 等比中项：、、成等比数列，或x GyGxyGxy 2 前项和：（要注意）nSnaqaqqqnn111111()()!  性质：是等比数列an （）若，则··1mnp qaaaamnpq （）， ， „„仍为等比数列2232SSSSSnnnnn （3）（时，，时，）naSnaSSnnn12111 2. 你熟悉求数列通项公式的常用方法吗？ 例如：（1）求差（商）法  如：满足„„aaaannnn121212251122 解：naa 1122151411时，，∴ naaannn 2121212215212211时，„„   12122得：nna ∴ann21 ∴annnn141221()() ［练习］  数列满足，，求aSSaaannnnn111534 （注意到代入得：aSSSSnnnnn1114  又，∴是等比数列，SSSnnn144 naSSnnnn23411时，„„· （2）叠乘法  例如：数列中，，，求aaaannannnn1131 解：aaaaaannaannnn213211122311·„„·„„，∴ 又，∴aann133 （3）等差型递推公式 由，，求，用迭加法aaf naaannn110( ) naafaafaaf nnn22321321时，„„„„两边相加，得：( )( )( ) aafff nn 123( )( )( )„„ ∴„„aafff nn 023( )( )( ) ［练习］  数列，，，求aaaanannnnn111132 （）ann12 31 （4）等比型递推公式 acad cdccdnn1010、 为常数，，， 可转化为等比数列，设 axc axnn1 acacxnn 11 令，∴()cxdxdc11 ∴是首项为，为公比的等比数列adcadccn 111 ∴·adcadccnn1111 ∴aadccdcnn1111 ［练习］  数列满足，，求aaaaannnn11934 （）ann84311 （5）倒数法 例如：，，求aaaaannnn11122 由已知得：1221211aaaannnn ∴11121aann 111121aan为等差数列，，公差为 11112121annn· ∴ann 21 3. 你熟悉求数列前 n 项和的常用方法吗？ 例如：...