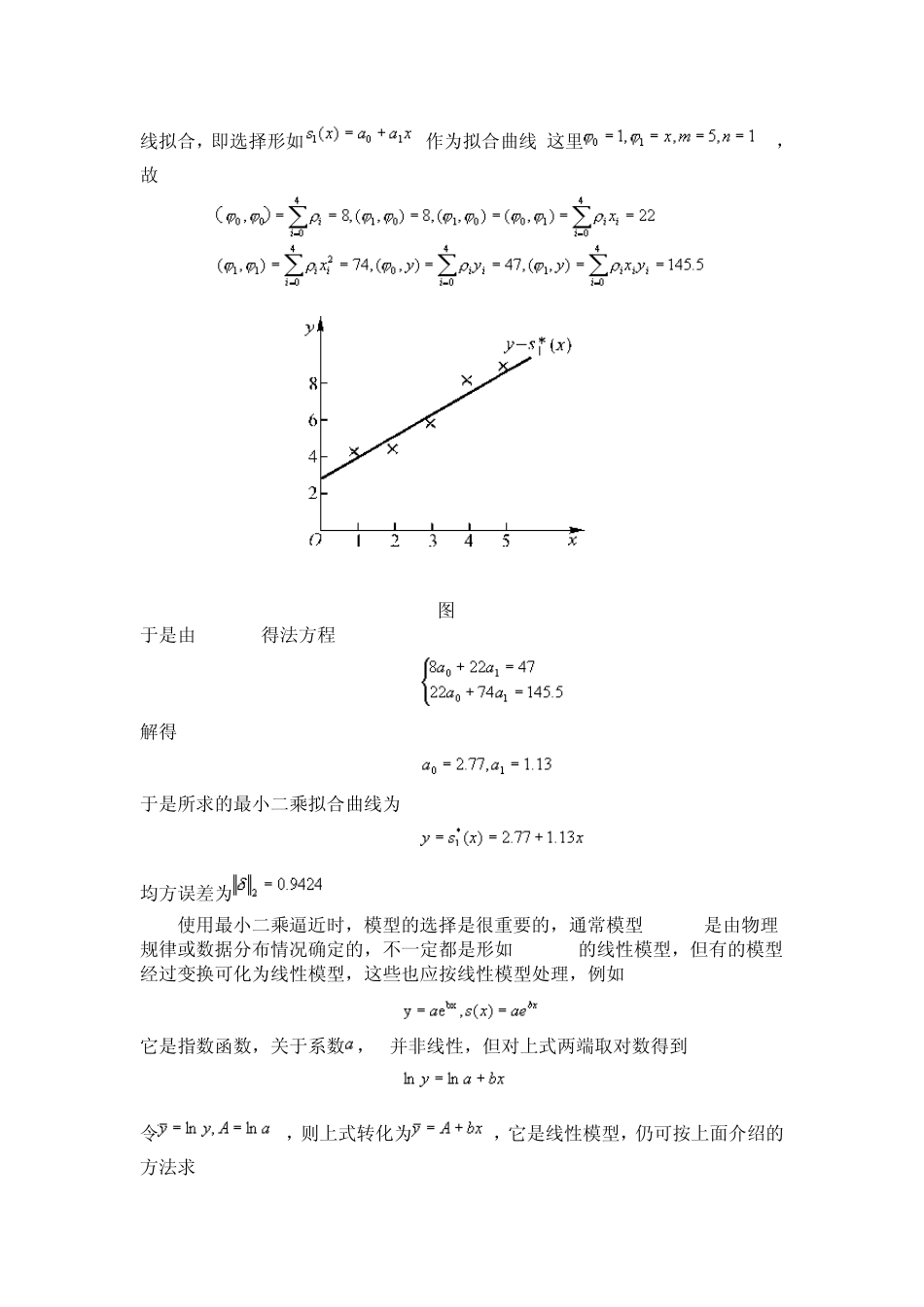
曲线拟合的最小二乘法 在科学实验数据处理中,往往要根据一组给定的实验数据,求出自变量x与因变量y的函数关系,这是 为待定参数,由于观测数据总有误差,且待定参数ai的数量比给定数据点的数量少(即 n<m),因此它不同于插值问题.这类问题不要求通过点,而只要求在给定点上的误差的平方和最小.当时,即 (5.8.1) 这里是线性无关的函数族,假定在上给出一组数据,以及对应的一组权,这里为权系数,要求使最小,其中 (5.8.2) 这就是最小二乘逼近,得到的拟合曲线为 y=s(x),这种方法称为曲线拟合的最小二乘法. (5.8.2)中实际上是关于的多元函数,求 I的最小值就是求多元函数I的极值,由极值必要条件,可得 (5.8.3) 根据内积定义(见第三章)引入相应带权内积记号 (5.8.4) 则(5.8.3)可改写为 这是关于参数的线性方程组,用矩阵表示为 (5.8.5) (5.8.5)称为法方程.当线性无关,且在点集上至多只有n 个不同零点,则称在X上满足Haar条件,此时(5.8.5)的解存在唯一(证明见[3]).记(5.8.5)的解为 从而得到最小二乘拟合曲线 (5.8.6) 可以证明对,有 故(5.8.6)得到的即为所求的最小二乘解.它的平方误差为 (5.8.7) 均方误差为 在最小二乘逼近中,若取,则,表示为 (5.8.8) 此时关于系数的法方程(5.8.5)是病态方程,通常当n≥3 时都不直接取作为基,其具体方法下节再讨论,下面只给出 n=1的例子. 例 5.10 已知一组实验数据如表所示. 试求最小二乘拟合曲线. 解 将所给数据在坐标纸上标出,如图 5-6所示,说明它可用线性函数作曲线拟合,即选择形如作为拟合曲线.这里,故 图5-6 于是由(5.8.5)得法方程 解得 于是所求的最小二乘拟合曲线为 均方误差为. 使用最小二乘逼近时,模型的选择是很重要的,通常模型y=s(x)是由物理规律或数据分布情况确定的,不一定都是形如(5.8.1)的线性模型,但有的模型经过变换可化为线性模型,这些也应按线性模型处理,例如 它是指数函数,关于系数,b并非线性,但对上式两端取对数得到 令,则上式转化为,它是线性模型,仍可按上面介绍的方法求y=s(x). 例5.11 给定数据如下: 求的最小二乘拟合曲线. 解 不是多项式,但两端取对数得.若令,则有,它是线性最小二乘拟合问题.可取,为求得A,b,先将 化为 .转化后的数据表为 根据最小二乘原理先求法方程系数 故有法方程 解得,于是得最小二乘拟合曲线 讲解: 曲线拟合的最小二乘法是处理实验数据一种经常使用的方法,它与插值不同,...