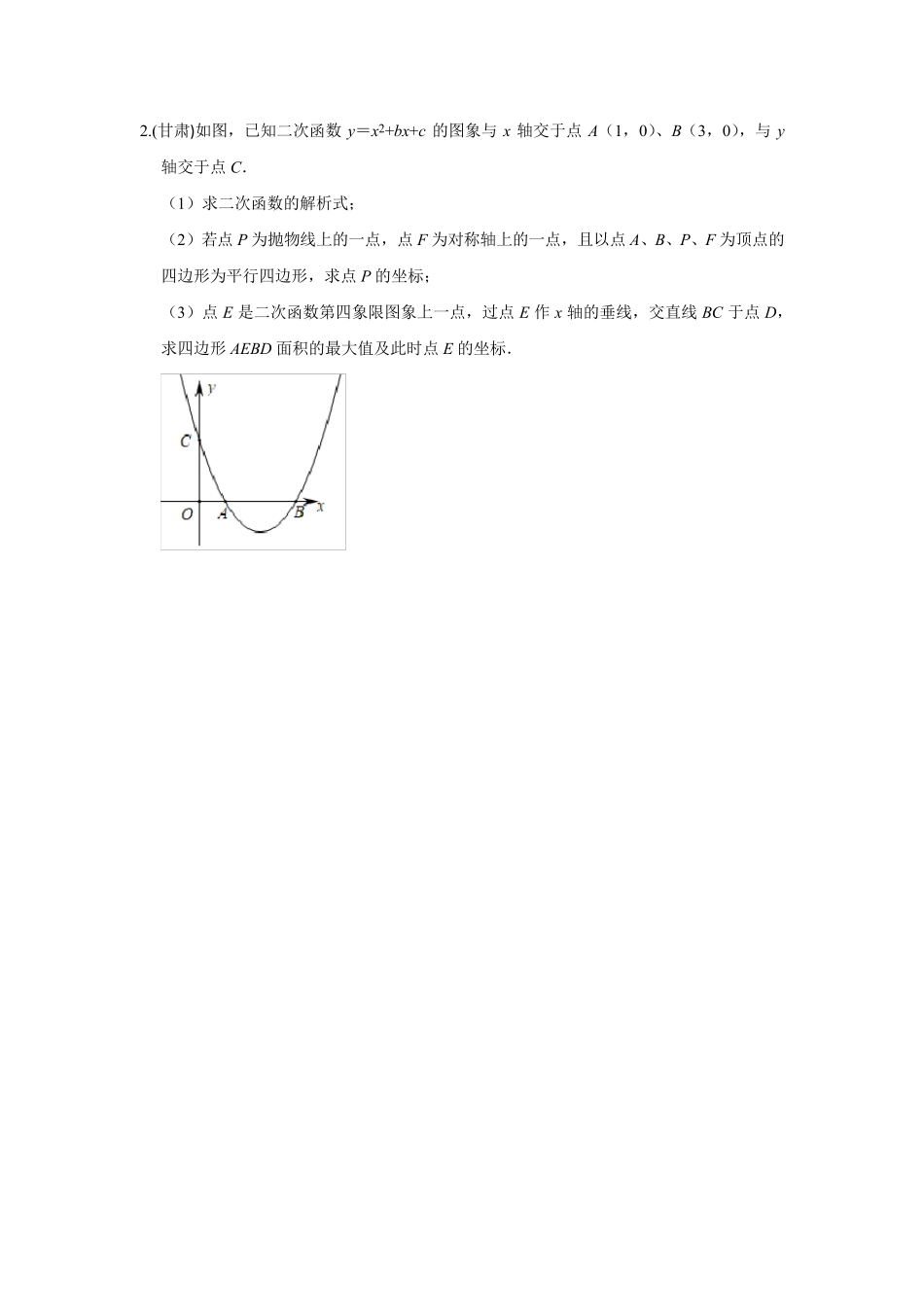
2019 中考数学压轴题 1.(眉山)如图1,在平面直角坐标系中,抛物线y=﹣94x2+bx+c 经过点A(﹣5,0)和点B(1,0). (1)求抛物线的解析式及顶点D 的坐标; (2)点P 是抛物线上A、D 之间的一点,过点P 作PE⊥x 轴于点E,PG⊥y 轴,交抛物线于点G.过点G 作GF⊥x 轴于点F.当矩形PEFG 的周长最大时,求点P 的横坐标; (3)如图2,连接AD、BD,点M 在线段AB 上(不与A、B 重合),作∠DMN=∠DBA, MN 交线段AD 于点N,是否存在这样点M,使得△DMN为等腰三角形?若存在,求出 AN的长;若不存在,请说明理由. B A C O D E F G P y x 图 1 图 2 A B C D y x M N O 2.(甘肃)如图,已知二次函数y=x2+bx+c 的图象与x 轴交于点A(1,0)、B(3,0),与y轴交于点C. (1)求二次函数的解析式; (2)若点P 为抛物线上的一点,点F 为对称轴上的一点,且以点A、B、P、F 为顶点的四边形为平行四边形,求点P 的坐标; (3)点E 是二次函数第四象限图象上一点,过点E 作 x 轴的垂线,交直线 BC 于点D,求四边形 AEBD 面积的最大值及此时点E 的坐标. 3 .(广安)如图,抛物线ᵆ = −ᵆ2 + ᵄᵆ + ᵅ与x 轴交于A、B 两点(ᵃ在 B 的左侧),与y 轴交于点 N,过 A 点的直线l:ᵆ = ᵅᵆ + ᵅ与y 轴交于点 C,与抛物线ᵆ = −ᵆ2 + ᵄᵆ + ᵅ的另一个交点为 D,已知ᵃ(−1,0),ᵃ(5, −6),P 点为抛物线ᵆ = −ᵆ2 + ᵄᵆ + ᵅ上一动点(不与A、D 重合). (1)求抛物线和直线l 的解析式; (2)当点 P 在直线l 上方的抛物线上时,过 P 点作ᵄᵃ//ᵆ轴交直线l 于点 E,作ᵄᵃ//ᵆ轴交直线l 于点 F,求ᵄᵃ + ᵄᵃ的最大值; (3)设 M 为直线l 上的点,探究是否存在点 M,使得以点 N、C,M、P 为顶点的四边形为平行四边形?若存在,求出点 M 的坐标;若不存在,请说明理由. 4 .(武威)如图,抛物线y=ax2+bx+4 交x 轴于A(﹣3,0),B(4,0)两点,与y 轴交于点C,连接AC,BC.点P 是第一象限内抛物线上的一个动点,点P 的横坐标为m. (1)求此抛物线的表达式; (2)过点P 作PM⊥x 轴,垂足为点M,PM 交BC 于点Q.试探究点P 在运动过程中,是否存在这样的点Q,使得以 A,C,Q 为顶点的三角形是等腰三角形.若存在,请求出此时点Q 的坐标,若不存在,请说明理由; (3)过点P 作PN⊥BC,垂足为点N.请用含 m 的代数...