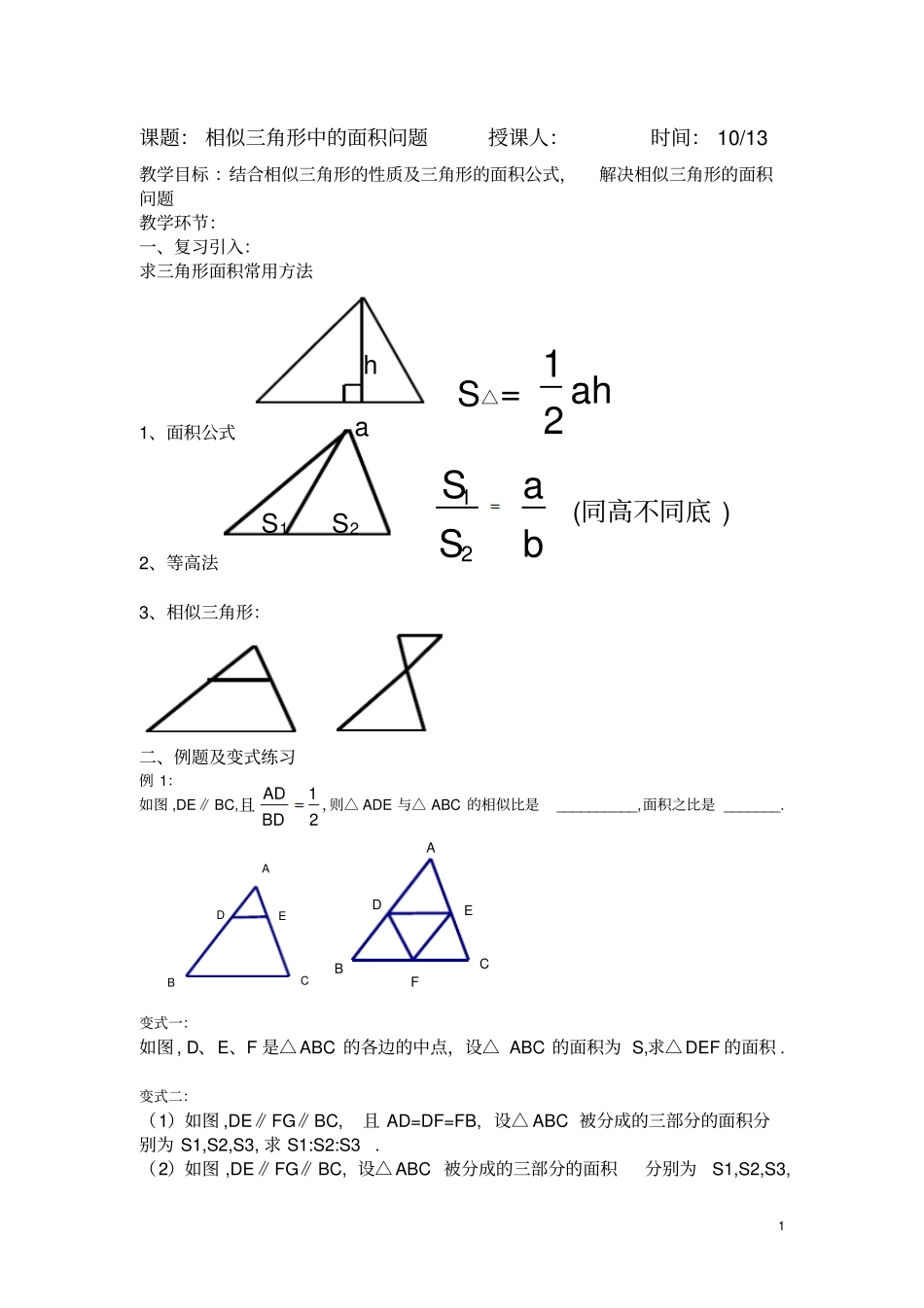
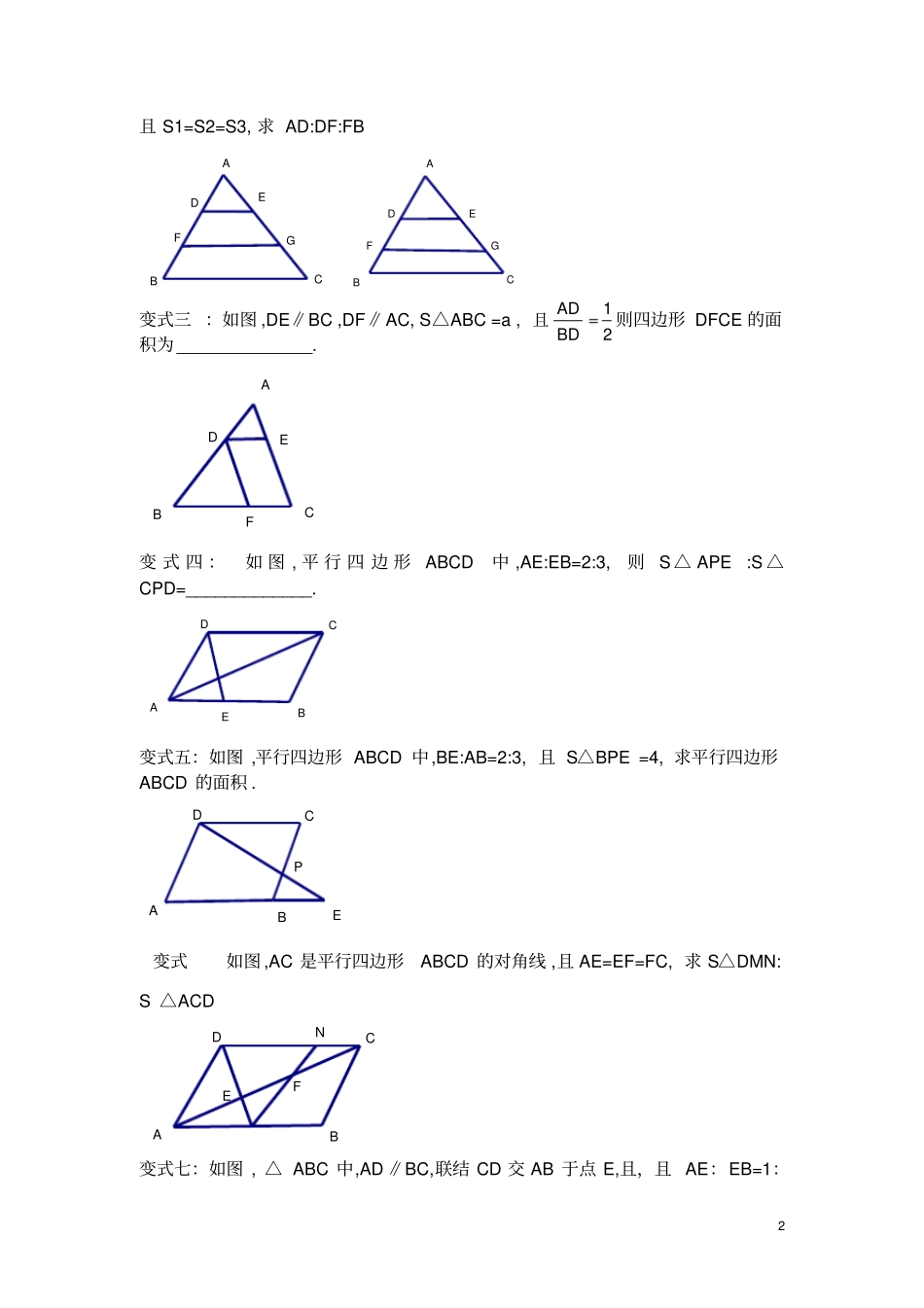
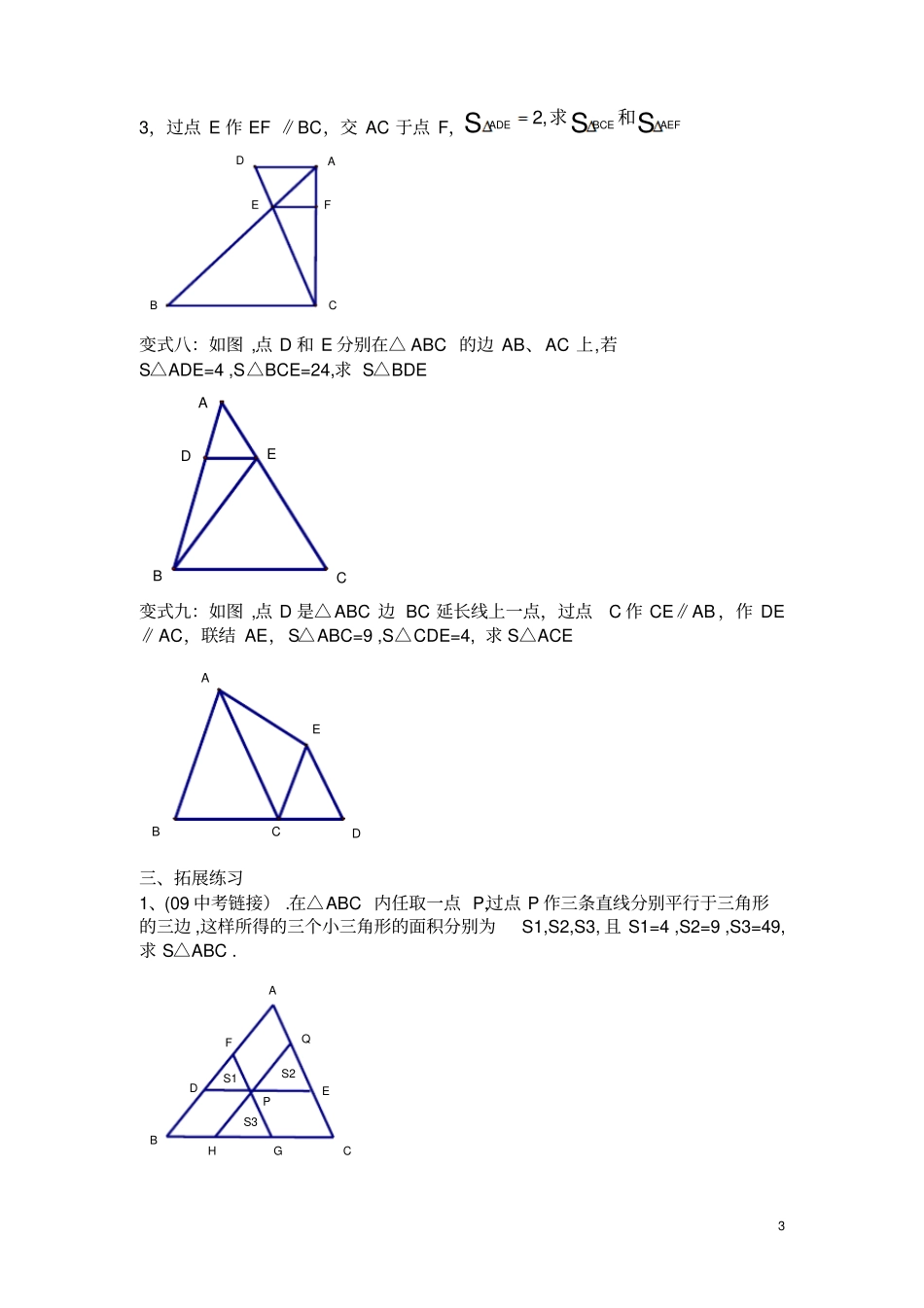
1 课题: 相似三角形中的面积问题授课人:时间: 10/13 教学目标 :结合相似三角形的性质及三角形的面积公式,解决相似三角形的面积问题教学环节:一、复习引入:求三角形面积常用方法1、面积公式2、等高法3、相似三角形:二、例题及变式练习例 1:如图 ,DE∥ BC, ,则△ ADE 与△ ABC 的相似比是__________,面积之比是 _______. CBEDAFCBEDA变式一:如图 , D、E、F 是△ ABC 的各边的中点,设△ ABC 的面积为 S,求△ DEF 的面积 .变式二:(1)如图 ,DE∥FG∥BC, 且 AD=DF=FB, 设△ ABC 被分成的三部分的面积分别为 S1,S2,S3, 求 S1:S2:S3 . (2)如图 ,DE∥FG∥ BC, 设△ ABC 被分成的三部分的面积分别为S1,S2,S3,a h S△= 12ah12SaSb(同高不同底 ) S1 S2 12ADBD且2 且 S1=S2=S3, 求 AD:DF:FB GFCBEDAAEDCGFB变式三 :如图 ,DE∥BC ,DF∥AC, S△ABC =a , 则四边形 DFCE 的面积为 ______________. FCBEDA变 式 四 :如 图 , 平 行 四 边 形ABCD中 ,AE:EB=2:3, 则S △ APE :S △CPD=_____________.DCBEA变式五:如图 ,平行四边形 ABCD 中,BE:AB=2:3, 且 S△BPE =4, 求平行四边形ABCD 的面积 . PDCBEA变式如图 ,AC 是平行四边形ABCD 的对角线 ,且 AE=EF=FC, 求 S△DMN: S △ACD NDCFBEA变式七:如图 , △ ABC 中,AD ∥BC,联结 CD 交 AB 于点 E,且,且 AE:EB=1:12ADBD且3 3,过点 E 作 EF ∥BC,交 AC 于点 F,变式八:如图 ,点 D 和 E 分别在△ ABC 的边 AB、AC 上,若S△ADE=4 ,S△BCE=24,求 S△BDE 变式九:如图 ,点 D 是△ ABC 边 BC 延长线上一点,过点C 作 CE∥AB ,作 DE∥AC,联结 AE,S△ABC=9 ,S△CDE=4, 求 S△ACE 三、拓展练习1、(09 中考链接) .在△ABC 内任取一点 P,过点 P 作三条直线分别平行于三角形的三边 ,这样所得的三个小三角形的面积分别为S1,S2,S3, 且 S1=4 ,S2=9 ,S3=49, 求 S△ABC . S3S2S1QFGHEPCBDADECBADECBAFDECBASSAEFBCE,2和求S ADE4 2、在△ ABC 中,D 为 BC 边上的中点 ,E 为 AC 边上任意一点 ,BE 交 AD 于点 O,请探究 : AOEDCBAOEDCB根据以上规律 ,你能求AOEDCBAOEDCB四、总结:1.找到与已知和所求有关的基本图形. 2.找到相似三角形及相似比利用面积比等于相似比的平方. 3 等高法①等底 ( 或同底 ) 的三角形面积之比等于高之比②等高 (或同高 )的三角形面积之比等于对应底之比. 12AOBDOBSAEACS如图 (1), 当时, 1(3),,4AOBDOBSAEACS如图当时1,1AOBDOBSAEACnS当时的值吗 ?1,3AOBDOBSAEACS如图 (2), 当时