流函数涡量法的二维方腔流数值模拟(matlab编程)

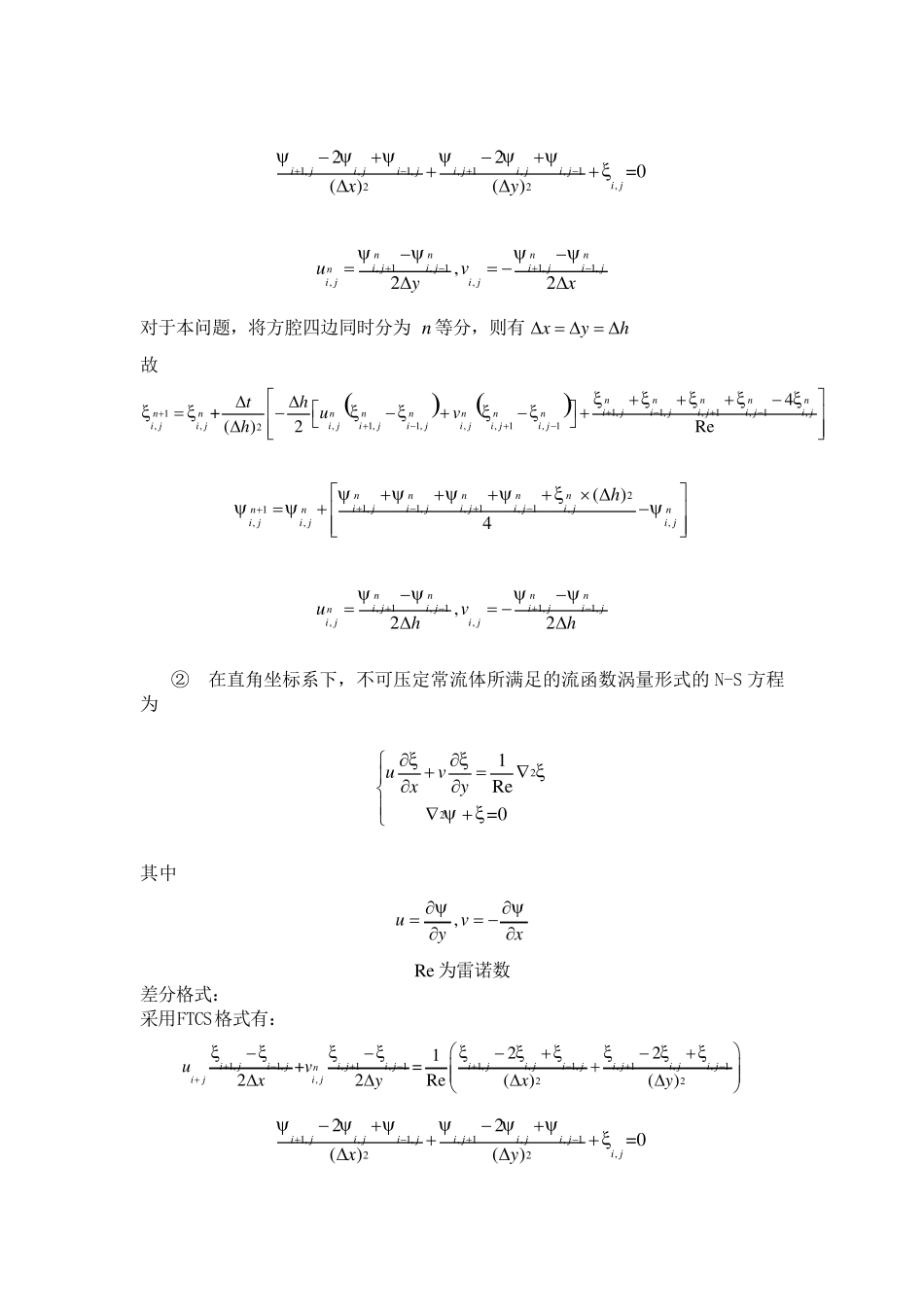
流函数- 涡量法的二维方腔流数值模拟 基本方程： ① 在直角坐标系下，不可压非定常流体所满足的流函数涡量形式的N-S 方程为 221Reuvtxy   其中 ,uvyx  Re为雷诺数 差分格式： 采用FTCS格式有： 1,,1,1,,1,11,,1,,1,,1,,2222122Re()()nnnnnnnnnnnni ji jijiji ji jiji jiji ji ji jnni ji juvtxyxy  1,,1,,1,,1,2222=0()()iji jiji ji ji ji jxy ,1,11,1,,,,22nnnni ji jijijni ji juvyx  对于本问题，将方腔四边同时分为n 等分，则有xyh     故 1,1,,1,1,1,,,1,1,,,1,124+ ()2Rennnnnijiji ji ji jnnnnnnnni ji ji jijiji ji ji jth uvh  21,1,,1,1,1,,,()4nnnnnijiji ji ji jnnni ji ji jh  ,1,11,1,,,,22nnnni ji jijijni ji juvhh  ② 在直角坐标系下，不可压定常流体所满足的流函数涡量形式的 N-S 方程为 221Re=0uvxy 其中 ,uvyx  Re为雷诺数 差分格式： 采用FTCS格式有： 1,1,,1,11,,1,,1,,1,22221+=22Re()()ijiji ji jiji jiji ji ji jniji juvxyxy 1,,1,,1,,1,2222=0()()iji jiji ji ji ji jxy ,1,11,1,,,,22i ji jijiji ji juvyx  对于本问题，将方腔四边同时分为n 等分，则有xyh     ，则有即 1,1,,1,11,,,1,1,,,1,1,Re=+48nnnnijiji ji jnnnnnnnnni ji ji jijiji ji ji ji jh uv 21,1,,1,1,1,,,()4nnnnnijiji ji ji jnnni ji ji jh  ,1,11,1,,,,22n...