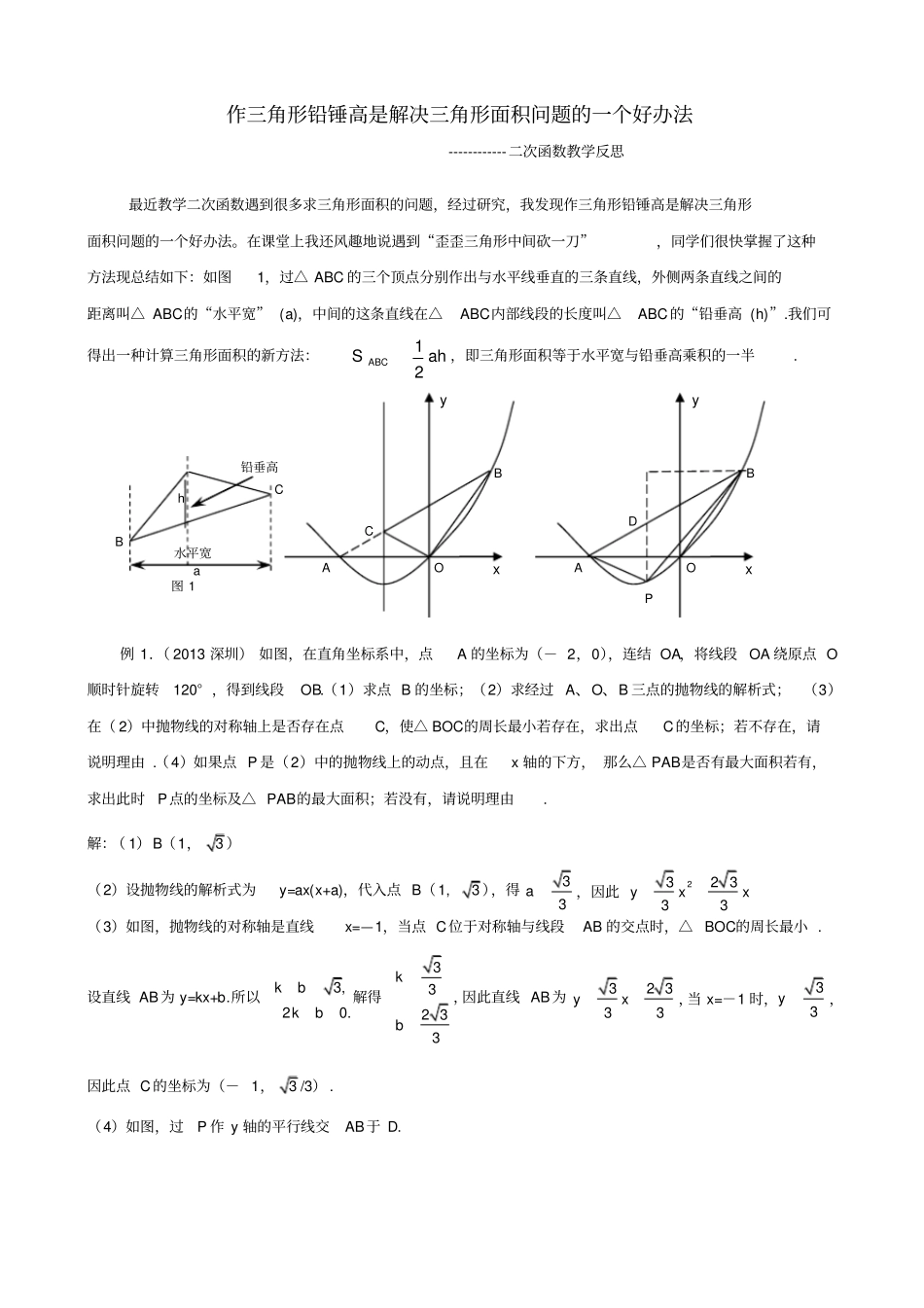
作三角形铅锤高是解决三角形面积问题的一个好办法------------二次函数教学反思最近教学二次函数遇到很多求三角形面积的问题,经过研究,我发现作三角形铅锤高是解决三角形面积问题的一个好办法。在课堂上我还风趣地说遇到“歪歪三角形中间砍一刀”,同学们很快掌握了这种方法现总结如下:如图1,过△ ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ ABC的“水平宽” (a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高 (h)”.我们可得出一种计算三角形面积的新方法:ahS ABC21,即三角形面积等于水平宽与铅垂高乘积的一半. 例 1.( 2013 深圳) 如图,在直角坐标系中,点A 的坐标为(- 2,0),连结 OA,将线段 OA 绕原点 O顺时针旋转120° ,得到线段OB.(1)求点 B 的坐标;(2)求经过 A、O、B 三点的抛物线的解析式;(3)在( 2)中抛物线的对称轴上是否存在点C,使△ BOC的周长最小若存在,求出点C的坐标;若不存在,请说明理由 .(4)如果点 P 是(2)中的抛物线上的动点,且在x 轴的下方, 那么△ PAB是否有最大面积若有,求出此时P点的坐标及△ PAB的最大面积;若没有,请说明理由.解:( 1)B(1,3 )(2)设抛物线的解析式为y=ax(x+a),代入点 B(1, 3 ),得33a,因此232 333yxx(3)如图,抛物线的对称轴是直线x=—1,当点 C位于对称轴与线段AB 的交点时,△ BOC的周长最小 .设直线 AB为 y=kx+b.所以33,320.2 33kkbkbb解得,因此直线 AB为32 333yx,当 x=-1 时,33y,因此点 C的坐标为(- 1,3 /3) .(4)如图,过P 作 y 轴的平行线交AB于 D.BC铅垂高水平宽h a 图 1CBAOyxDBAOyxP2221 ()()2132 332 332333333322319 3228PABPADPBDDPBASSSyyxxxxxxxx当 x=- 12时,△ PAB的面积的最大值为938,此时13,24P.例 2.(2014 益阳 ) 如图 2,抛物线顶点坐标为点C(1,4),交 x 轴于点 A(3,0),交 y 轴于点 B.(1)求抛物线和直线 AB 的解析式; (2)点 P 是抛物线 (在第一象限内 )上的一个动点,连结PA,PB,当 P点运动到顶点C时,求△ CAB的铅垂高 CD 及CABS;(3)是否存在一点P,使 S△PAB=89 S△ CAB,若存在,求出P 点的坐标;若不存在,请说明理由.解: (1)设抛物线的解析式为:4)1(21xay把 A(3,0)代入解析式求得1a所以324)1(221xxxy设直线 AB的解析式为:bkxy2由3221xxy求得B 点的坐标为)3,0...