自适应第三章模型参考自适应控制VIP免费

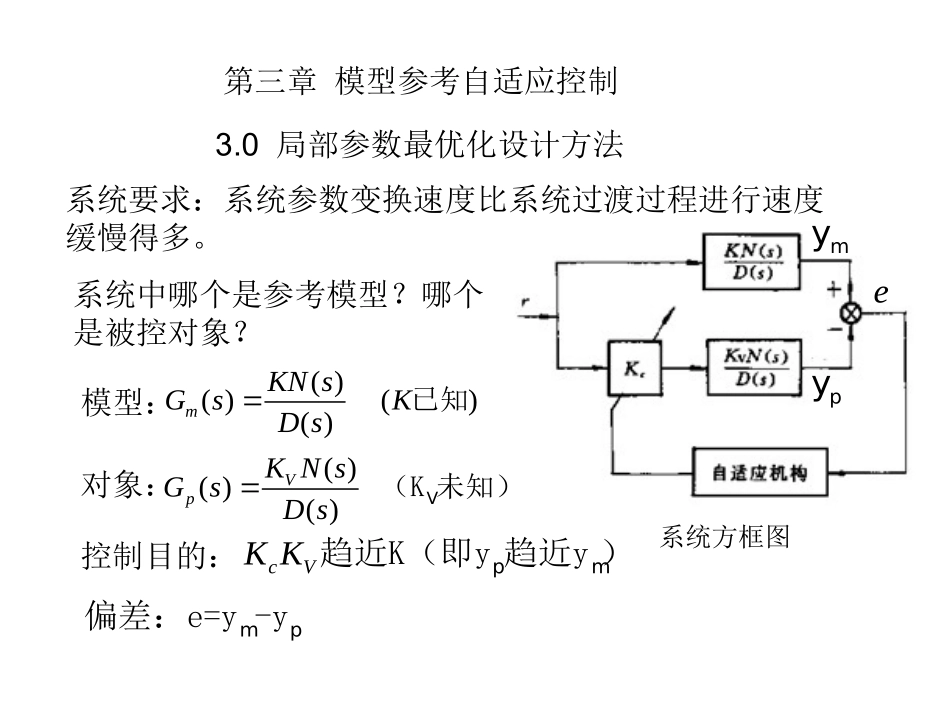
第三章模型参考自适应控制3.0局部参数最优化设计方法系统要求：系统参数变换速度比系统过渡过程进行速度缓慢得多。系统方框图模型：对象：()()()()mKNsGsKDs已知系统中哪个是参考模型？哪个是被控对象？()()()VpKNsGsDsV（K未知）控制目的：cVKKpm趋近K（即y趋近y）pymyemp偏差：e=y-y性能指标：21()2Jed（按J最小来确定自适应律）求偏导：ccJeedKK梯度法：规定负梯度方向是函数下降最快的方向。0()cJKc即K其中为调整步长－常数cJKcc0K-KcJKcc0KKceedKc0KceeKcK系统开环传函：()()()cVeNsKKKrDs,dpdt令得微分方程的时域算子形式（用p代s）()()()cVDpeKKKNprcK对求偏导：()()(1)VceDpKNprK模型微分方程：()()myKNsrDs()()(2)mDpyKNpr(1)/(2):VmcKeyKK得:VcmKKeyKc代入K中，得VmKeyKVKK令＝cmKey0cmcKeydtK（自适应律）0cmcKeydtK－MIT方案：乘法器、积分器组成mypyemyMIT自适应控制方案图缺点：稳定性得不到保证，要检验稳定性（保证e收敛）。优点：设计方法简单，易于实现。例：设控制对象的微分算子方程为：221(1)()()pVapapytKrt参考模型的微分算子方程为：221(1)()()mapapytKrt试按MIT方案，求自适应律。解：设自适应可调增益为Kc，则得：21()mmmayayyKrt21()pppcVayayyKKrt相减：21()()cVaeaeeKKKrt（输出误差方程）cmKey自适应律：检验稳定性：胡尔维茨（hurwitz）稳定判据设系统特征方程为：11100nnnnasasasa稳定充要条件：主行列式1352413200000000000nnnnnnnnnaaaaaaaaaa及其主对角线上的各子行列式0i110na即13220nnnnaaaa1353241300nnnnnnnnaaaaaaaa0n假设r(t)为阶跃信号，r(t)=R，并设KV缓慢变化，0VK过渡过程很短，在e的调节过程中，ym(t)已达稳定值，即myKR21()VcaeaeeKKrt求导：21cVmKaeaeeKyre代入，得：myKR210VaeaeeKKRre由hurwitz判据：13210100VVaKKRraaKKRr110a12201VaKKRra12VaaKKRr3012VaaKKRr12VaaKKRr10a3.1一阶系统的模型参考自适应控制被控对象：()()()pppYskPsUssa参考模型：()()()mmmmYskMsRssappak其中：、为未知参数mmak，按理想的输出响应选取0mmak其中：，>0图：一阶系统模型参考自适应控制控制目标：设计控制信号u(t),使对象输出yp(t)渐近跟踪参考模型的输出ym(t)，且所有系统中的信号有界。时域描述：被控对象：参考模型：()ppppyaykut()mmmmyaykrt控制信号：00()()()()()putctrtdtyt00[()()()()]pppppyaykctrtdtyt**00,pmmppaakcdkk令：**000(),()tcdtd0则c时[()()]pmmpppppppaakyaykrtytkk()()()ppmpmpaykrtaayt()()mpmaytkrt传函：()()pmmYskRssa∴可调系统与模型传函完全匹配。(参数希望值)0pmeyy输出误差：令参数误差：*0*0()()()()rytctctdtd0pmeyy00pppppmmmaykcrkdyaykr00mpmpmmpppppmayayayaykcrkdykr00()()()mpmmppppmayyaakdykckr**00000[()()]mppaekddyccr0()mpypraekyr0()()tdt0任务：设计c、的自适应律，使方程渐近稳定，即t时0()0,0,0yret。判断稳定性：1、选李氏函数22200(,,)()()22pryrykeVeg正定0,0pkg其中：2、求导0002(,,)(22)22pryrryykeVeeg0000[()]()pmpyprrykeaekyrcdg200000prpympypprkkaekeykercdgg200000()()mpypprdcaekeykergg0000()()0pypprdckeykergg...