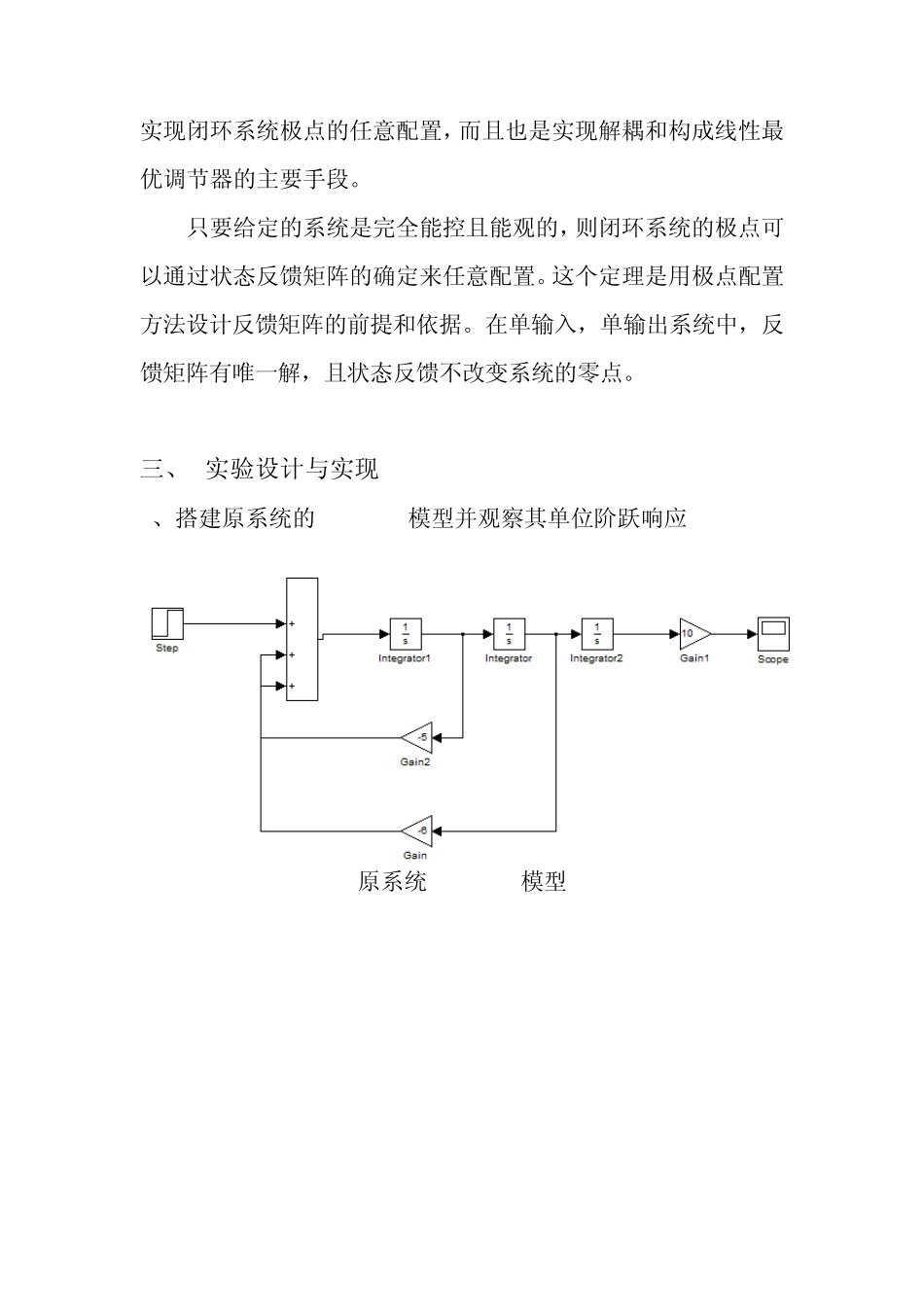
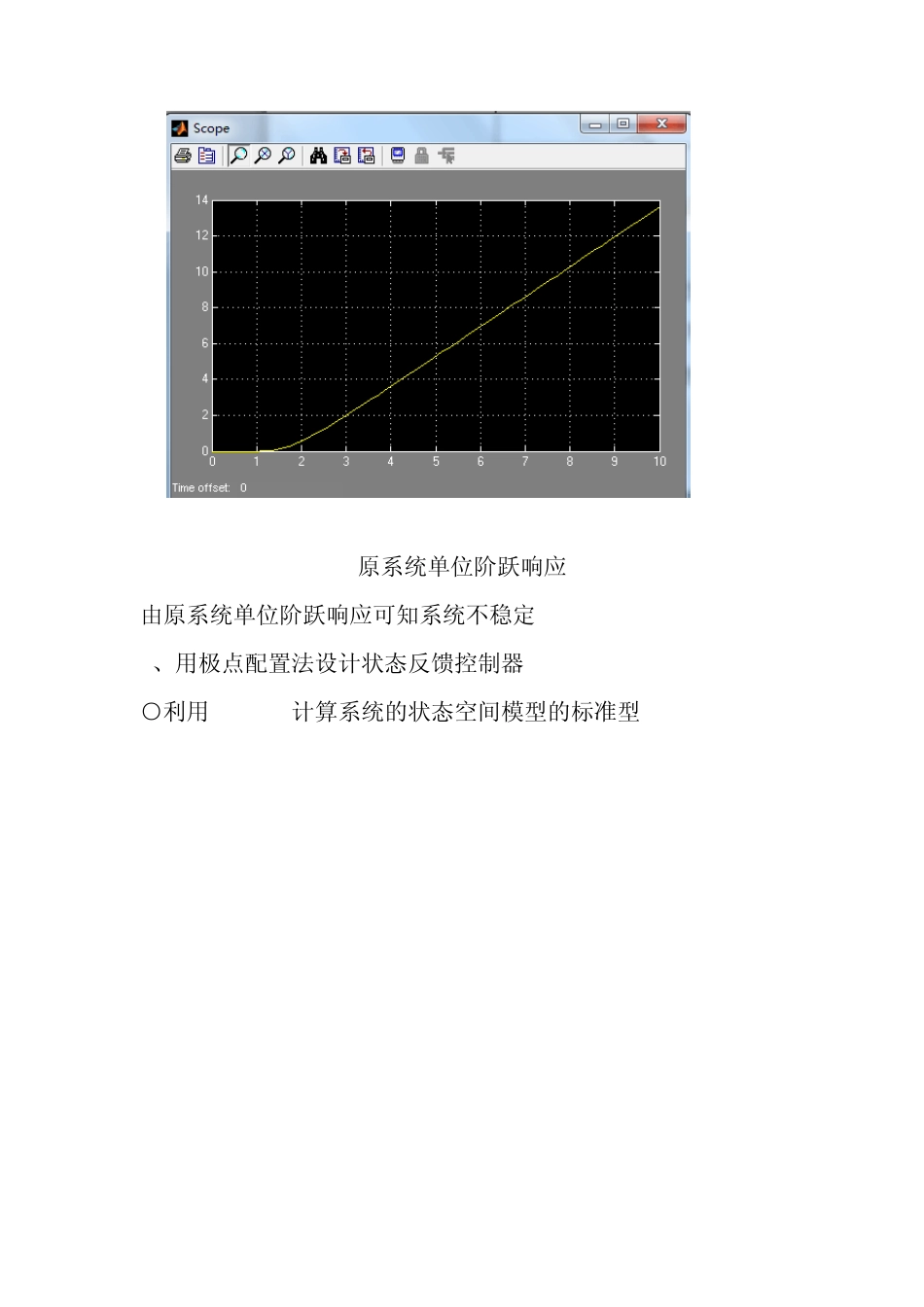
上海电力学院实验报告 自动控制原理实验课程 题目:状态反馈控制器的设计 班级: 姓名: 学号: 时间: 一、 问题描述 已知一个单位反馈系统的开环传递函数为,试搭建simulink模型。仿真原系统的阶跃响应。再设计状态反馈控制器,配置系统的闭环极点在,并用 simulink 模型进行仿真验证。 二、 理论方法分析 MATLAB提供了单变量系统极点配置函数 acker(),该函数的调用格式为 K=place(A,b,p) 其中,P为期望闭环极点的列向量,K为状态反馈矩阵。Acker()函数时Ackerman公式编写,若单输入系统可控的,则采用状态反馈控制后,控制量 u=r+Kx。 对于多变量系统的状态反馈极点配置,MATLAB也给出了函数 place(),其调用格式为 K=place(A,B,P) 状态反馈是将系统的状态变量乘以相应的反馈系数,然后反馈到输入端与参考输入叠加形成控制量,作为受控系统的输入,实现闭环系统极点的任意配置,而且也是实现解耦和构成线性最优调节器的主要手段。 只要给定的系统是完全能控且能观的,则闭环系统的极点可以通过状态反馈矩阵的确定来任意配置。这个定理是用极点配置方法设计反馈矩阵的前提和依据。在单输入,单输出系统中,反馈矩阵有唯一解,且状态反馈不改变系统的零点。 三、 实验设计与实现 1、搭建原系统的sumlink模型并观察其单位阶跃响应 原系统sumlink模型 原系统单位阶跃响应 由原系统单位阶跃响应可知系统不稳定 2、用极点配置法设计状态反馈控制器 ○1利用matlab计算系统的状态空间模型的标准型 >> a=[10];b=[1 5 6 0];[A B C D]=tf2ss(a,b) A = -5 -6 0 1 0 0 0 1 0 B = 1 0 0 C = 0 0 10 D = 0 ○2系统能控性矩阵 >> uc=ctrb(A,B) uc = 1 -5 19 0 1 -5 0 0 1 >> rank(uc) ans = 3 所以系统完全能控 ○3系统能观型矩阵 >> vo=obsv(A,C) vo = 0 0 10 0 10 0 10 0 0 >> rank(vo) ans = 3 所以系统完全能观 所以可以用极点配置法设计状态反馈控制器 ○4求解系统反馈矩阵 >> p=[-3 -0.5+j -0.5-j];k=acker(A,B,p) k = -1.0000 -1.7500 3.7500 加入反馈后的系统闭环极点为: >>sysnew=ss(A-B*k,B,C,D);pole(sysnew) ans = -3.0000 -0.5000 + 1.0000i -0.5000 - 1.0000i ○5搭建加入反馈控制器后系统的 sumlink模型 ○6观察新系统的单位阶跃响应 四、 实验结果分析 加入反馈控制器后系统的闭环极点在,符合题目要求。所以实验结果为正确。 五、 结论与讨论 这次实验做的是用 MATLAB 函数设计合适的状态变量反馈。首先老师让我们用手算的方法做了一遍,后来又用 MATLAB 算了一遍,得到了相同的结果,总之实验进行的很成功,这是最后一次实验了,这门实验课让我掌握了 MATLAB 的基本用法,收益很多。