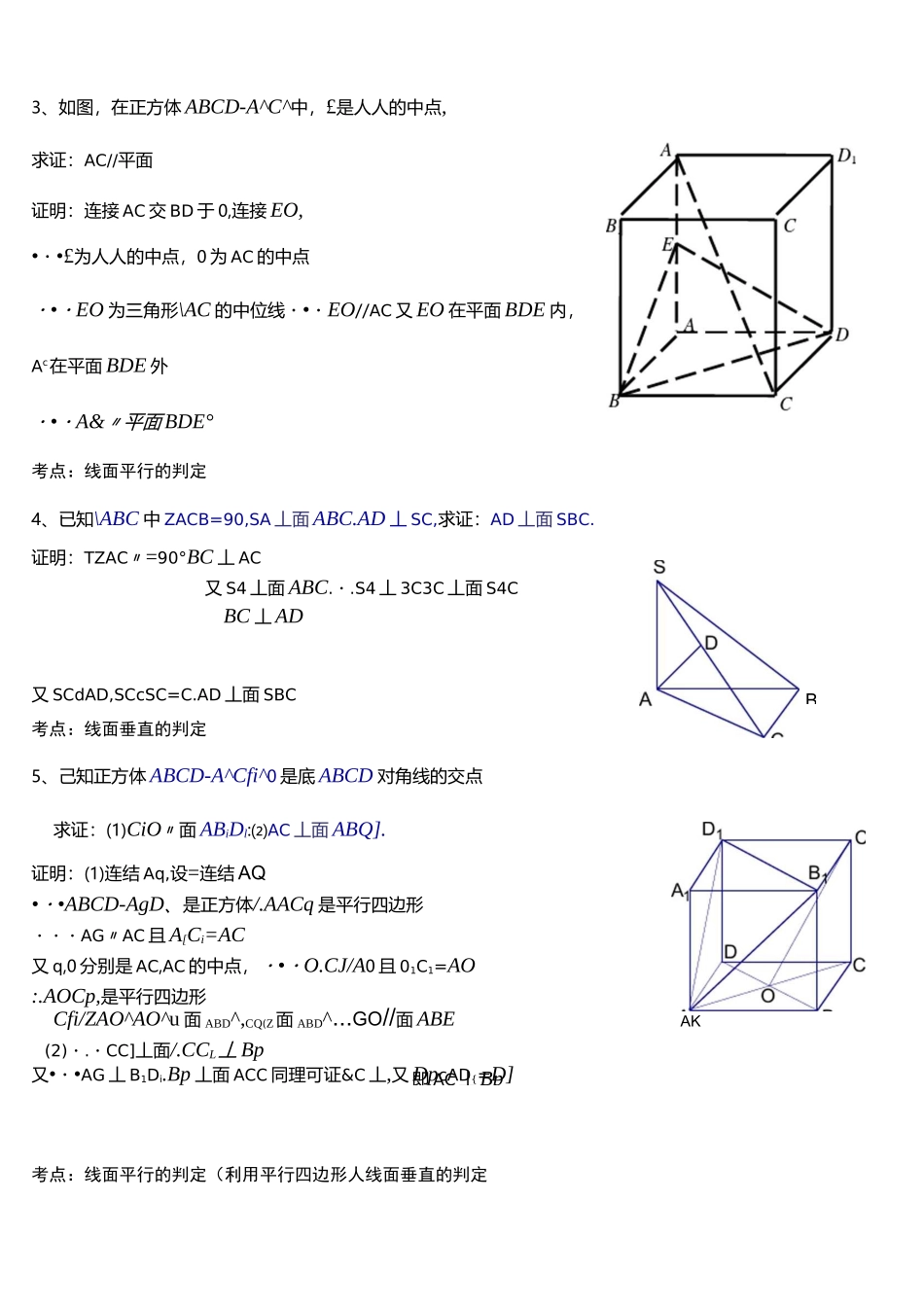
高考立体几何常考经典证明题锦集1.己知四边形 ABCD 是空间四边形,EFG.H 分别是边 AB.BC.CD.DA 的中点(1)求证:EFGH 是平行四边形(2)若 BD=2>/3,AC 二 2,EG 二 2。求异面直线 AC、BD 所成的角和 EG、BD 所成的角。又•••AB^平面 ABC9•••平面 CDE 丄平 WiABC考点^线面垂直,面面垂直的判定证明:在△MD 中,IE.H 分别是 AB.AD 的中点 AEH//BD.EH==BD2同理,FG//BD、FG=-BD:.EH//FG、EH=FG:.四边形 EFGH 是平行四边形。2(2)90°30°考点:证平行(利用三角形中位线),异面直线所成的角2、如图,已知空间四边形 ABCD 中,BC=AC,AD=BD,E 是 4〃的中点。求证:(1)丄平面 CDE;(2)平面 CDE 丄平面 ABC.A证明:BC=AC\=>CE±AB又:・CEcDE=EAE=BE(2)由(1)有 A3 丄平面 CDE即 AC 丄 Bp3、如图,在正方体 ABCD-A^C^中,£是人人的中点,求证:AC//平面证明:连接 AC 交 BD 于 0,连接 EO,•・•£为人人的中点,0 为 AC 的中点・•・EO 为三角形\AC 的中位线・•・EO//AC 又 EO 在平面 BDE 内,Ac在平面 BDE 外・•・A&〃平面 BDE°考点:线面平行的判定4、已知\ABC 中 ZACB=90,SA 丄面 ABC.AD 丄 SC,求证:AD 丄面 SBC.证明:TZAC〃=90°BC 丄 AC又 S4 丄面 ABC.・.S4 丄 3C3C 丄面 S4CBC 丄 AD又 SCdAD,SCcSC=C.AD 丄面 SBC考点:线面垂直的判定5、己知正方体 ABCD-A^Cfi^0 是底 ABCD 对角线的交点求证:(1)CiO〃面 ABiDl:⑵AC 丄面 ABQ].证明:(1)连结 Aq,设=连结 AQ•・•ABCD-AgD、是正方体/.AACq 是平行四边形・・・AG〃AC 且 A[Ci=AC又 q,0 分别是 AC,AC 的中点,・•・O.CJ/A0 且 01C1=AO:.AOCp,是平行四边形Cfi/ZAO^AO^u 面 ABD^,CQ(Z面 ABD^...GO//面 ABE(2)・.・CC]丄面/.CCL丄 Bp又•・•AG 丄 B1Di.Bp 丄面 ACC 同理可证&C 丄,又 DpcAD{=D]考点:线面平行的判定(利用平行四边形人线面垂直的判定BAK6、正方体 ABCD-A^B^C^D1中,求证:(1)4C 丄平面(2)3D 丄平面考点:线面垂直的判定7、正方体 ABCD—AiBiCiD 中.(1)求证:平面 A/D〃平面 BQQ⑵ 若£、F 分别是人纸,CG 的中点,求证:平面 EBQJ/平面 FBD.证明:⑴由 B\B//DD、,得四边形 BBQQ 是平行四边形,:・BD〃BD,又 3D(Z 平面BiDiC,BQ1U 平面 BLDC,・・・BD〃平面 5DC.同理 AQ〃平面 BLDLC.而•••平面 AiBD〃平面 BCD.(2)由 BD//BD,得 BD〃...