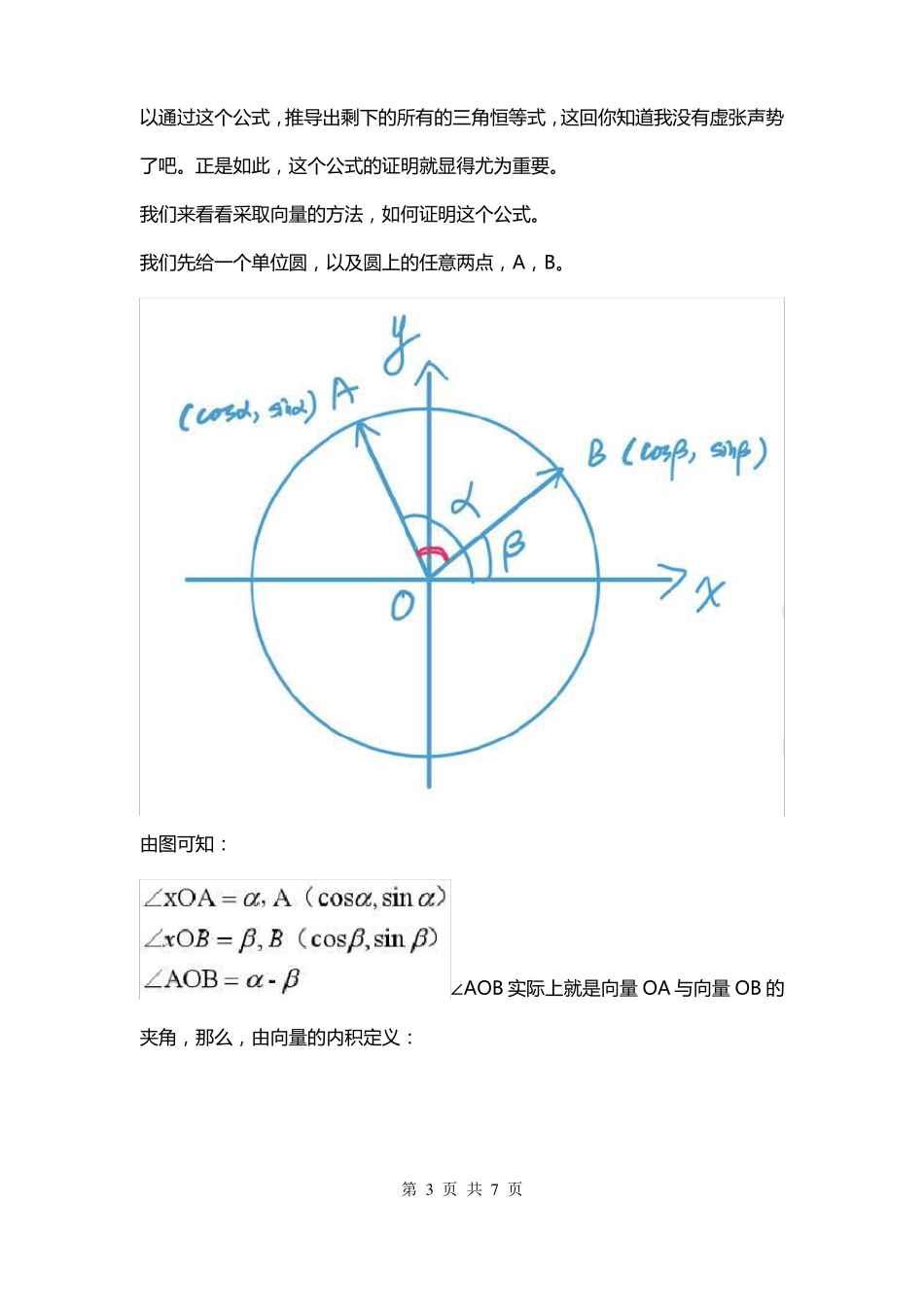
向量在高中数学里的妙用姓名:__________指导:__________日期:__________第 1 页 共 7 页向量,顾名思义,就是既有方向又有大小的量,在物理里面又称为矢量。物理里面,像位移、速度、加速度、力等物理量,都是矢量。从向量的定义,我们不难看出,向量具有几何方面的特性——方向,又具有代数方面的特性——大小。这就意味着,向量先天然的就是一个代数与几何完美结合的典范,具有很强的解析性。这也意味着,向量问题的处理,经常体现数形结合的思想,很多时候是比较灵活的,需要我们多加琢磨。其实在以前的高中数学教材里,是没有向量这一模块的知识的。对于向量,我们数学老师的感受是非常深刻的,因为向量的引入,极大程度上降低了某些传统知识的讲解和学习,像三角恒等式、余弦定理、柯西不等式等等。毫不夸张的说,向量就是一把利器,既利于老师教学,也利于学生学习。然而,遗憾的是,部分老师自己不太接受这个新的工具(其实也不新了,向量引入高中教材,已经有 16 年之久了),还是用传统的方法来讲解上述定理(余弦定理等)。诚然,传统的方法也体现了很丰富的数学思想,但较之向量还是要逊色一些。再者,我们常常鼓励孩子们要接受新知识,新方法,我们老师又何尝不是如此呢。今天,我们就来讲讲,采用向量这个工具,如何在上述定理的学习中发挥巧妙的作用,一起来感受向量在数形结合里展现的奇妙。一、两角余弦差公式先来看看两角余弦差公式的表述形式:我们知道,在所有三角恒等式里,两角余弦差公式是最重要的公式,没有之一!为什么?因为可第 2 页 共 7 页以通过这个公式,推导出剩下的所有的三角恒等式,这回你知道我没有虚张声势了吧。正是如此,这个公式的证明就显得尤为重要。我们来看看采取向量的方法,如何证明这个公式。我们先给一个单位圆,以及圆上的任意两点,A,B。由图可知:∠AOB 实际上就是向量 OA 与向量 OB 的夹角,那么,由向量的内积定义:第 3 页 共 7 页因为 AB 两点在单位圆上,所以这两个向量的模都是 1,所以:如此,我们就用向量证明了两角的余弦差公式,是不是非常简洁啊。大家感兴趣的话,可以搜索一下传统的证明方式,是比较繁琐的。二、余弦定理余弦定理是解三角形里一个非常重要的定理,用向量的方式也是极其的简洁。在三角形 ABC 中,余弦定理表述如下:我们给一个三角形,当然,这是任意给的三角形,再给三个向量,即向量 AB,向量 AC,向量 BC。第 4 页 共 7 ...