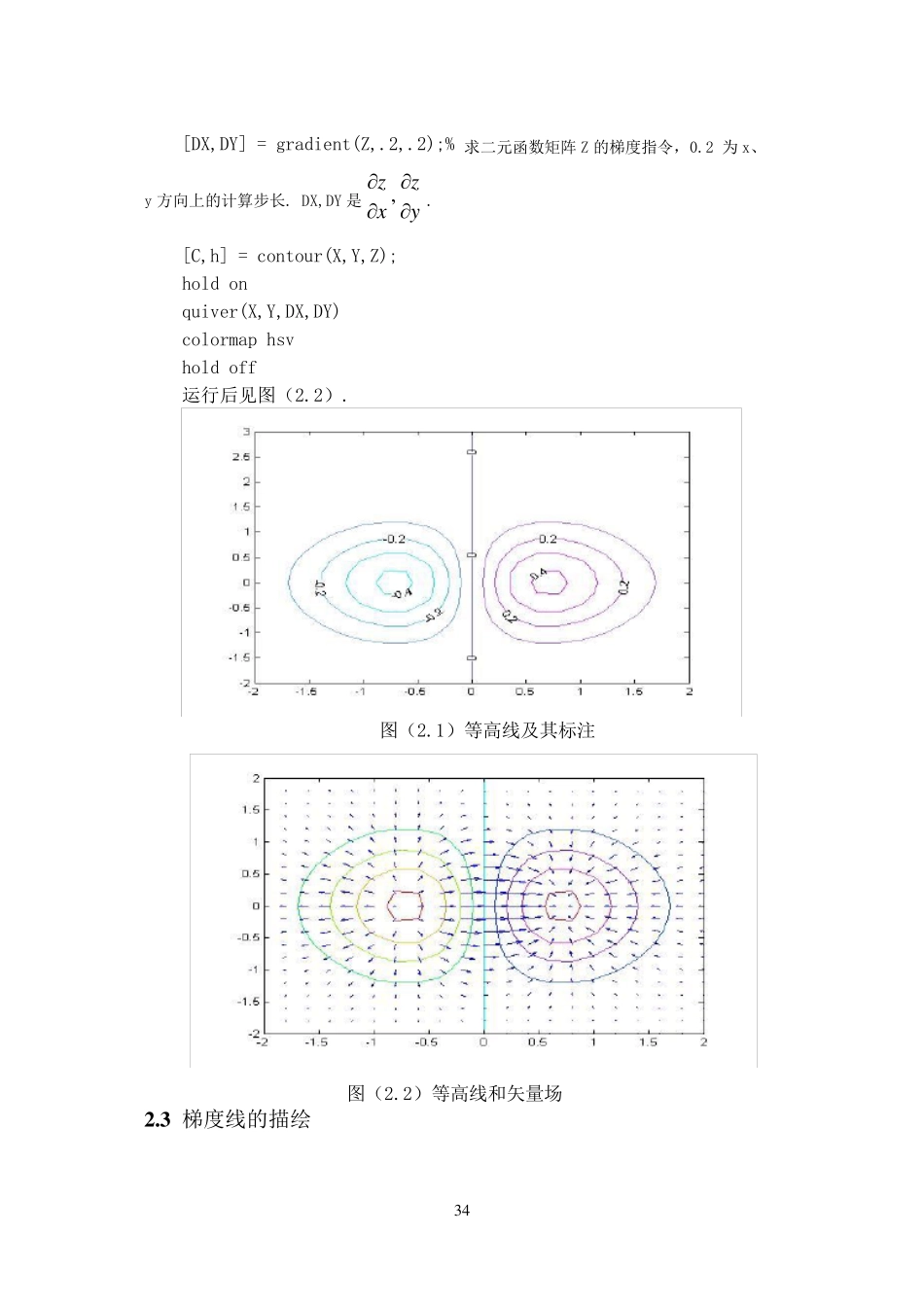
3 3 第二讲 函数的等高线、梯度线及有关的作图问题 ——鲨鱼袭击目标的前进途径 等高线和梯度线有广泛的实际应用,例如在地理学中绘制地貌图,在气象学中绘制气象图等等.本实验通过鲨鱼袭击目标这一例子介绍二元函数的等高线和梯度线的绘制,最后介绍用等高线来做一元隐函数的图形及微分方程的积分曲线. 2 .1 等高线的绘制 二元函数),(yxfz 在空间表示的是一张曲面,这个曲面与平面cz 的交线在 xoy 面上的投影曲线cyxf),(称为函数),(yxfz 的一条等高线,我们可以用 Matlab 作出等高线的图形. 等高线的作图命令为“Contour”,最基本格式为 Contour[二元函数,{自变量 1,自变量 1 最小值,自变量 1 最大值},{自变量 2,自变量 2 最小值,自变量 2 最大值}] 例 1 作出)(22yxxez在区间32,22yx上的等高线. 解 [X,Y] = meshgrid(-2:.2:2,-2:.2:3); Z = X.*exp(-X.^2-Y.^2); [C,h] = contour(X,Y,Z); set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2) colormap cool 运行后见图(2.1). 2 .2 矢量场图 矢量场图(又称速度图)是指由指令 quiver 实现的.它主要用于描写函数),(yxfz 在点),(yx的梯度大小和方向。其一般的调用格式为: quiver(X,Y,DZX,DZY) 例 2 作出函数)(22yxxez的等高线和矢量场. 解 [X,Y] = meshgrid(-2:.2:2,-1:.2:2); Z = X.*exp(-X.^2 - Y.^2); 3 4 [DX,DY] = gradient(Z,.2,.2);% 求二元函数矩阵Z 的梯度指令,0.2 为x、y 方向上的计算步长. DX,DY 是yzxz ,. [C,h] = contour(X,Y,Z); hold on quiver(X,Y,DX,DY) colormap hsv hold off 运行后见图(2.2). 图(2.1)等高线及其标注 图(2.2)等高线和矢量场 2 .3 梯度线的描绘 3 5 设L 为平面曲线,如果L 上任意一点处的切线与函数),(yxfz 在该店处的梯度位于同一直线上,则称L 为),(yxfz 的梯度线。现在来讨论如何作出函数),(yxfz 的梯度线。下面我们一等步长的折线段来近似模 拟函数的梯度线。设步长为 ,从点0P (00 , yx)出发,沿梯度方向前进 得到点 ),(111yxP,即 ),(),(),(0020020001yxfyxfyxfxxyxx),(),(),(0020020001yxfyxfyxfyyyxy, 再从),(111yxP出发沿梯度线向前进 得到点),(222yxP,依次得到一列点,利用"plot"做出此点集的图形,即得梯度线的图形. 例 3.作出函...