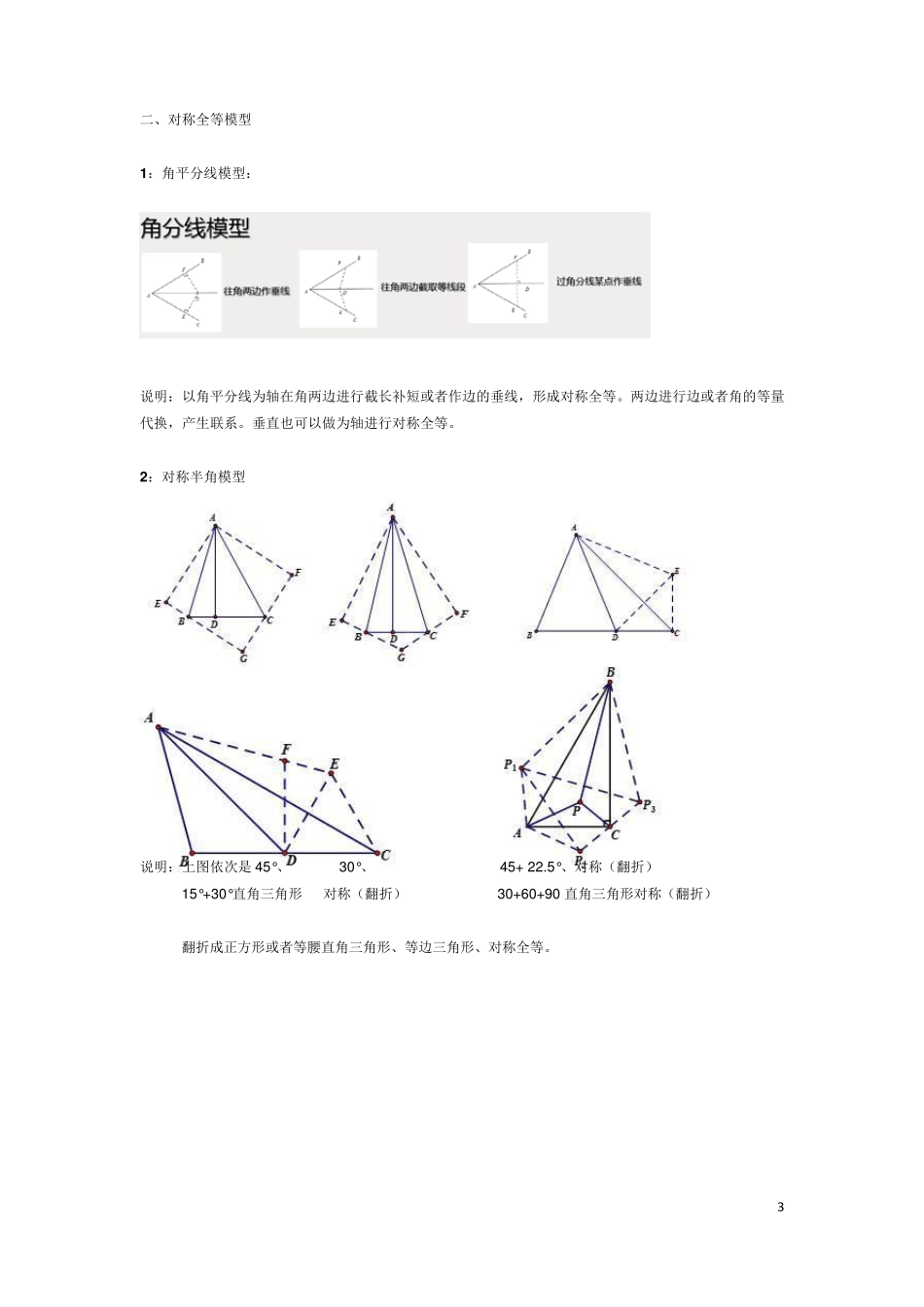
1 初二数学 三角形全等 常用几何模型及构造方法大全 掌握它轻松搞定 全等 题! 全等是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间,这次整理了常用的各大模型,一定要认真掌握~ 全等变换类型: (一) 平移全等:平行等线段(平行四边形) (二)对称全等模型:角平分线或垂直或半角 1 :角平分线模型; 2 :对称半角模型; (三)旋转全等模型:相邻等线段绕公共顶点旋转 1. 旋转半角模型 2. 自旋转模型 3. 共旋转模型 4 . 中点旋转 2 一、平移 全等变换 如图,在△ABC 的边上取两点 D、E,且 BD=CE,求证:AB+AC>AD+AE 分析:将△ACE 平移使 EC 与 BD 重合。B\D,上方交点,左右两个三角形,两边和 大于 第三边! 3 二、对称全等模型 1 :角平分线模型: 说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。两边进行边或者角的等量代换,产生联系。垂直也可以做为轴进行对称全等。 2 :对称半角模型 说明:上图依次是 45°、 30°、 45+ 22.5°、对称(翻折) 15°+30°直角三角形 对称(翻折) 30+60+90 直角三角形对称(翻折) 翻折成正方形或者等腰直角三角形、等边三角形、对称全等。 4 三、旋转全等模型 1 . 半角:有一个角含 1 /2 角及相邻线段 2 . 自旋转:有一对相邻等线段,需要构造旋转全等 3 . 共旋转:有两对相邻等线段,直接寻找旋转全等(共顶点) 4 . 中点旋转:倍长中点相关线段转换成旋转全等问题(专题七) 1 、旋转半角模型 说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。 2 、自旋转模型 构造方法: 遇 6 0 度旋 6 0 度,造等边三角形 遇 9 0 度旋 9 0 度,造等腰直角 遇等腰旋顶点,造旋转全等 遇中点旋 1 8 0 度,造中心对称 5 3 、共旋转模型 说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。通过“8”字模型可以证明。 (接上------共旋转模型 ) 模型变形 说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形混用。 当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。 6 4 、中点旋转: 说明: 两个...