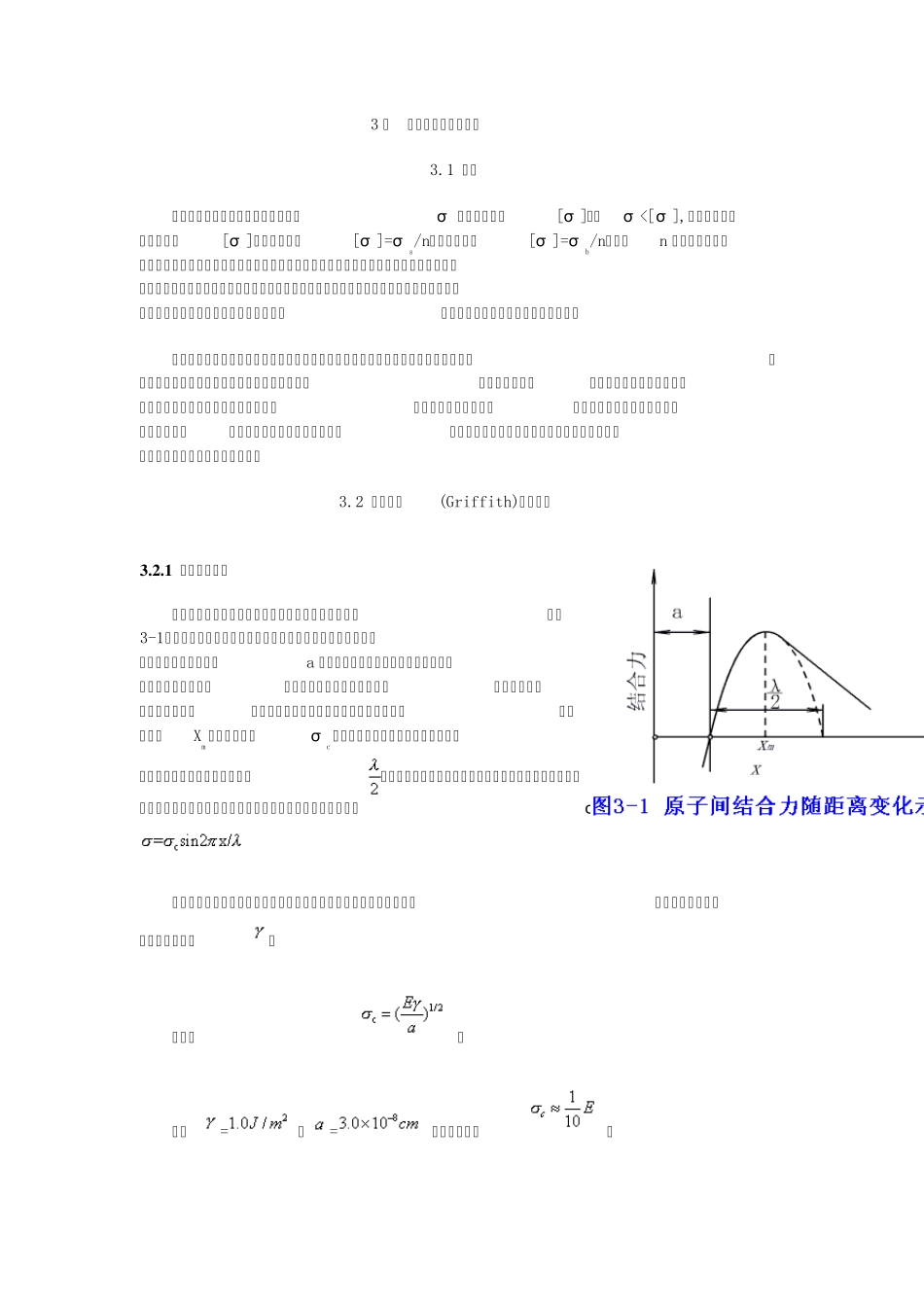
3 章 断裂力学与断裂韧性 3.1 概述 按照传统力学设计,只要求工作应力σ 小于许用应力[σ ],即σ <[σ ],就被认为是安全的了。而[σ ],对塑性材料[σ ]=σs/n,对脆性材料[σ ]=σb/n,其中n 为安全系数。经典的强度理论无法解释为什么工作应力远低于材料屈服强度时会发生所谓低应力脆断的现象。原来,传统力学是把材料看成均匀的,没有缺陷的,没有裂纹的理想固体,但是实际的工程材料,在制备、加工及使用过程中, 都会产生各种宏观缺陷乃至宏观裂纹。 人们在随后的研究中发现低应力脆断总是和材料内部含有一定尺寸的裂纹相联系的,当裂纹在给定的作用应力下扩展到一临界尺寸时,就会突然破裂。因为传统力学或经典的强度理论解决不了带裂纹构件的断裂问题,断裂力学就应运而生。可以说断裂力学就是研究带裂纹体的力学,它给出了含裂纹体的断裂判据,并提出一个材料固有性能的指标——断裂韧性,用它来比较各种材料的抗断能力。 3.2 格里菲斯(Griffith)断裂理论 3 .2 .1 理论断裂强度 金属的理论断裂强度可由原子间结合力的图形算出,如图3-1。图中纵坐标表示原子间结合力,纵轴上方为吸引力下方为斥力,当两原子间距为a 即点阵常数时,原子处于平衡位置,原子间的作用力为零。如金属受拉伸离开平衡位置,位移越大需克服的引力越大,引力和位移的关系如以正弦函数关系表示,当位移达到Xm 时吸力最大以σc 表示,拉力超过此值以后,引力逐渐减小,在位移达到正弦周期之半时,原子间的作用力为零,即原子的键合已完全破坏,达到完全分离的程度。可见理论断裂强度即相当于克服最大引力σc。该力和位移的关系为 图中正弦曲线下所包围的面积代表使金属原子完全分离所需的能量。分离后形成两个新表面,表面能为。 可得出 。 若以=,=代入,可算出。 3.2.2 格里菲斯(Griffith)断裂理论 金属的实际断裂强度要比理论计算的断裂强度低得多,粗略言之,至少低一个数量级,即。 陶瓷、玻璃的实际断裂强度则更低。 实际断裂强度低的原因是因为材料内部存在有裂纹。玻璃结晶后,由于热应力产生固有的裂纹;陶瓷粉末在压制烧结时也不可避免地残存裂纹。金属结晶是紧密的,并不是先天性地就含有裂纹。金属中含有裂纹来自两方面:一是在制造工艺过程中产生,如锻压和焊接等;一是在受力时由于塑性变形不均匀,当变形受到阻碍(如晶界、第二相等)产生了很大的应力集中,当应力集中达到理论断裂强度,而材料又不能通过塑性变形使...