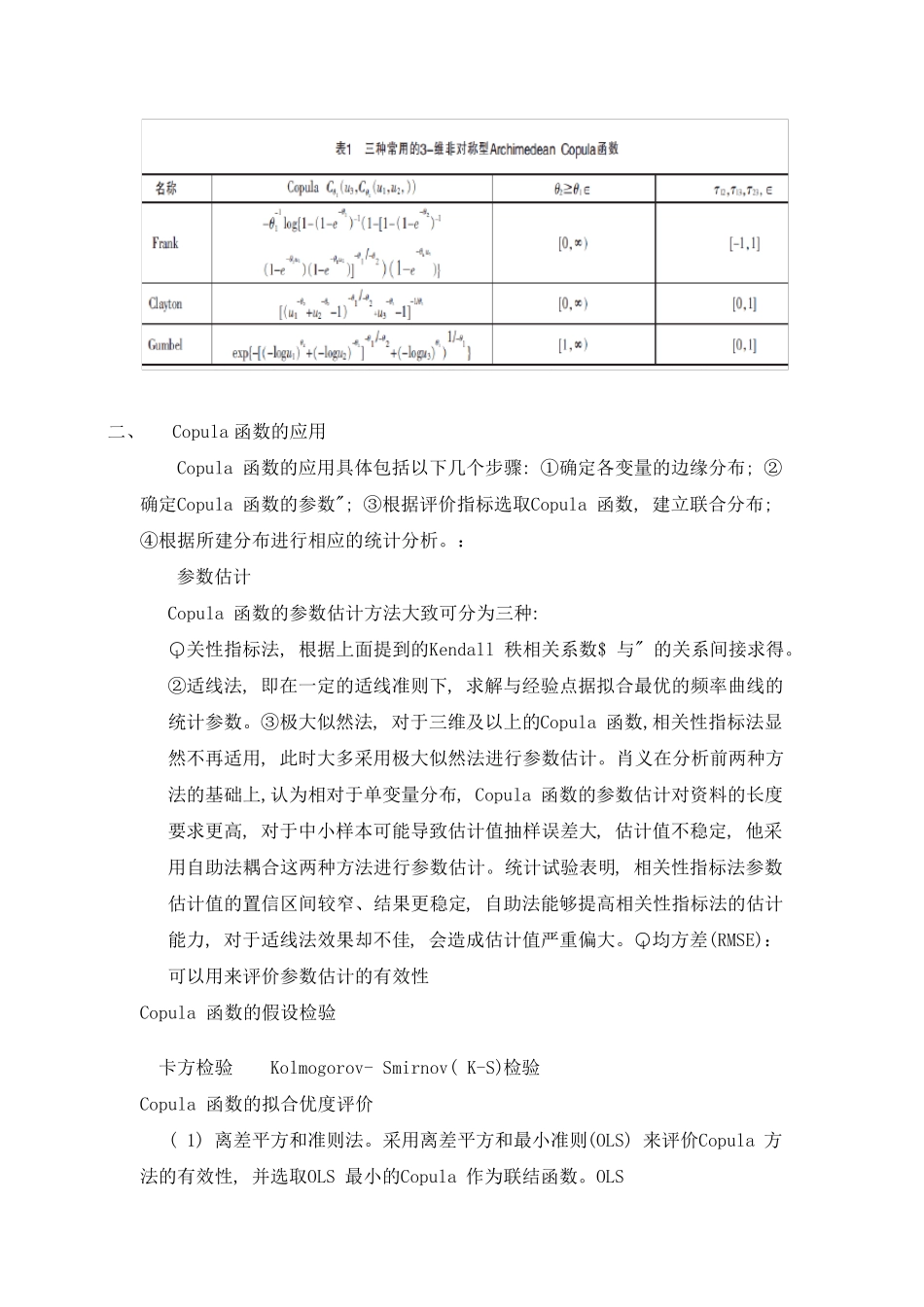
一、 Copula 函数理论 Copula 理论的是由Sklar 在1959 年提出的,Sklar 指出,可以将任意一个n 维联合累积分布函数分解为n 个边缘累积分布和一个Copula 函数。边缘分布描述的是变量的分布,Copula 函数描述的是变量之间的相关性。也就是说,Copula 函数实际上是一类将变量联合累积分布函数同变量边缘累积分布函数连接起来的函数,因此也有人称其为“连接函数”。 Copula 函数是定义域为[0,1]均匀分布的多维联合分布函数,他可以将多个随机变量的边缘分布连.起来得到他们的联合分布。 Copula 函数的性质 定理1 (Sklar 定理1959) 令 F 为一个n 维变量的联合累积分布函数,其中各变量的边缘累积分布函数记为Fi,那么存在一个n 维Copula 函数C,使得 111( , ,)( ( ), ,( ))nnnF xxC F xF x (1) 若边缘累积分布函数Fi是连续的,则 Copula 函数C 是唯一的。不然,Copula 函数C 只在各边缘累积分布函数值域内是唯一确定的。 对于有连续的边缘分布的情况,对于所有的[0,1]nu,均有 1111( )(( ),,())nnCF FuFuu (2) 在有非减的边缘变换绝大多数的 从Sklar 定理可以看出, Copula 函数能独立于随机变量的边缘分布反映随机变量的相关性结构, 从而可将联合分布分为两个独立的部分来分别处理: 变量间的相关性结构和变量的边缘分布, 其中相关性结构用Copula 函数来描述。Copula 函数的优点在于不必要求具有相同的边缘分布, 任意边缘分布经Copula 函数连接都可构造成联合分布, 由于变量的所有信息都包含在边缘分布里, 在转换过程中不会产生信息失真。 Copula 函数总体上可以划分为三类: 椭圆型、Archimedean(阿基米德) 型和二次型, 其中含一个参数的Archimedean Copula 函数应用最为广 泛 , 多维Archimedean Copula 函数的构造通 常 是基于二维的,根 据 构造方 式 的不同可以分为对称型和非对称型两种 . 三种 常 用的3-维非对称型Archimedean Copula函数: Frank Archimedean Copula函数 , Clayton Archimedean Copula函数, Gumbe Archimedean Copula函数 二、 Copula 函数的应用 Copula 函数的应用具体包括以下几个步骤: ①确定各变量的边缘分布; ②确定Copula 函数的参数"; ③根据评价指标选取Copula 函数, 建立联合分布; ④根据所建分布进行相应的统计分析。: 参数估计 Copula 函数的参数估计方法大致可分为...