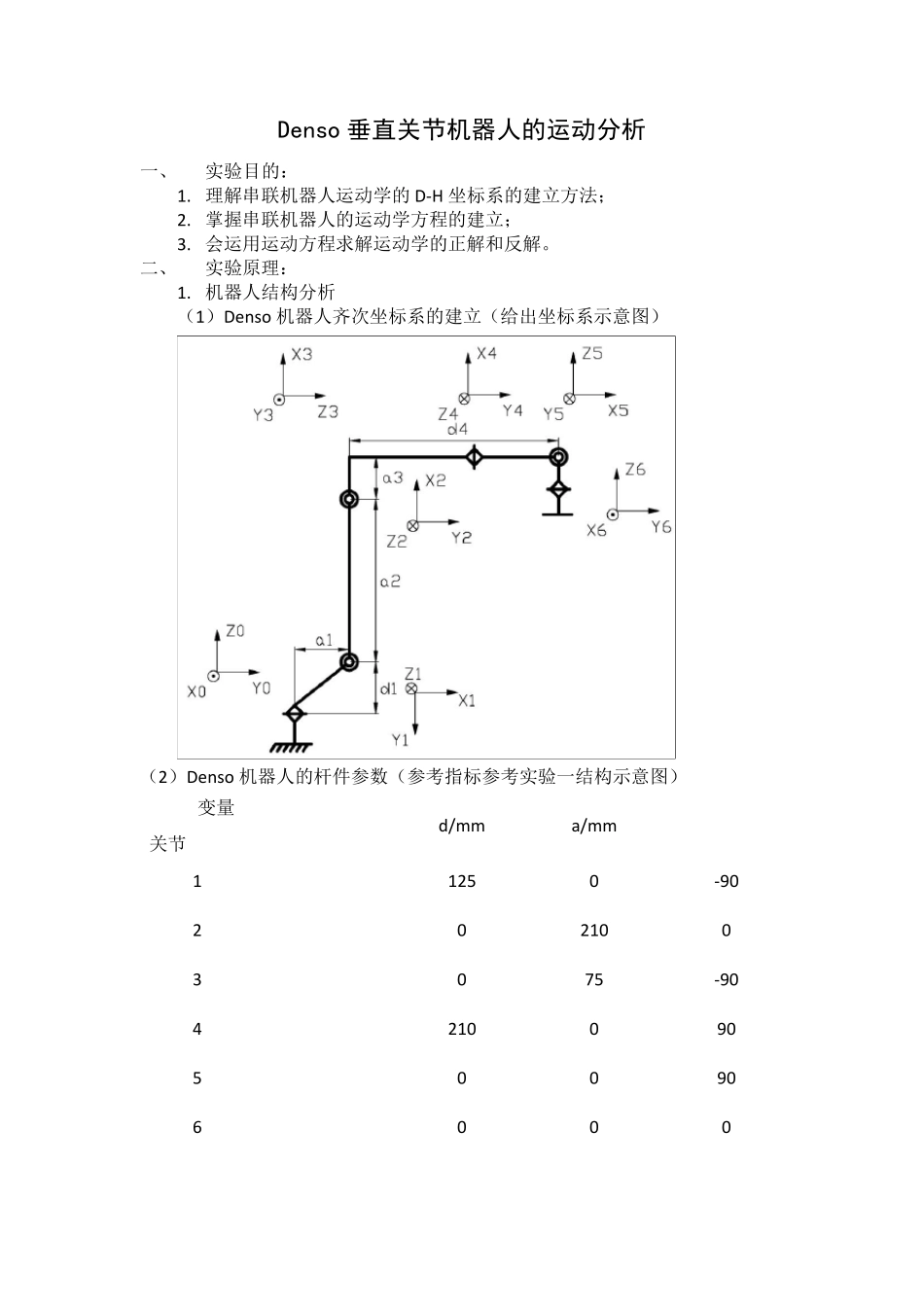
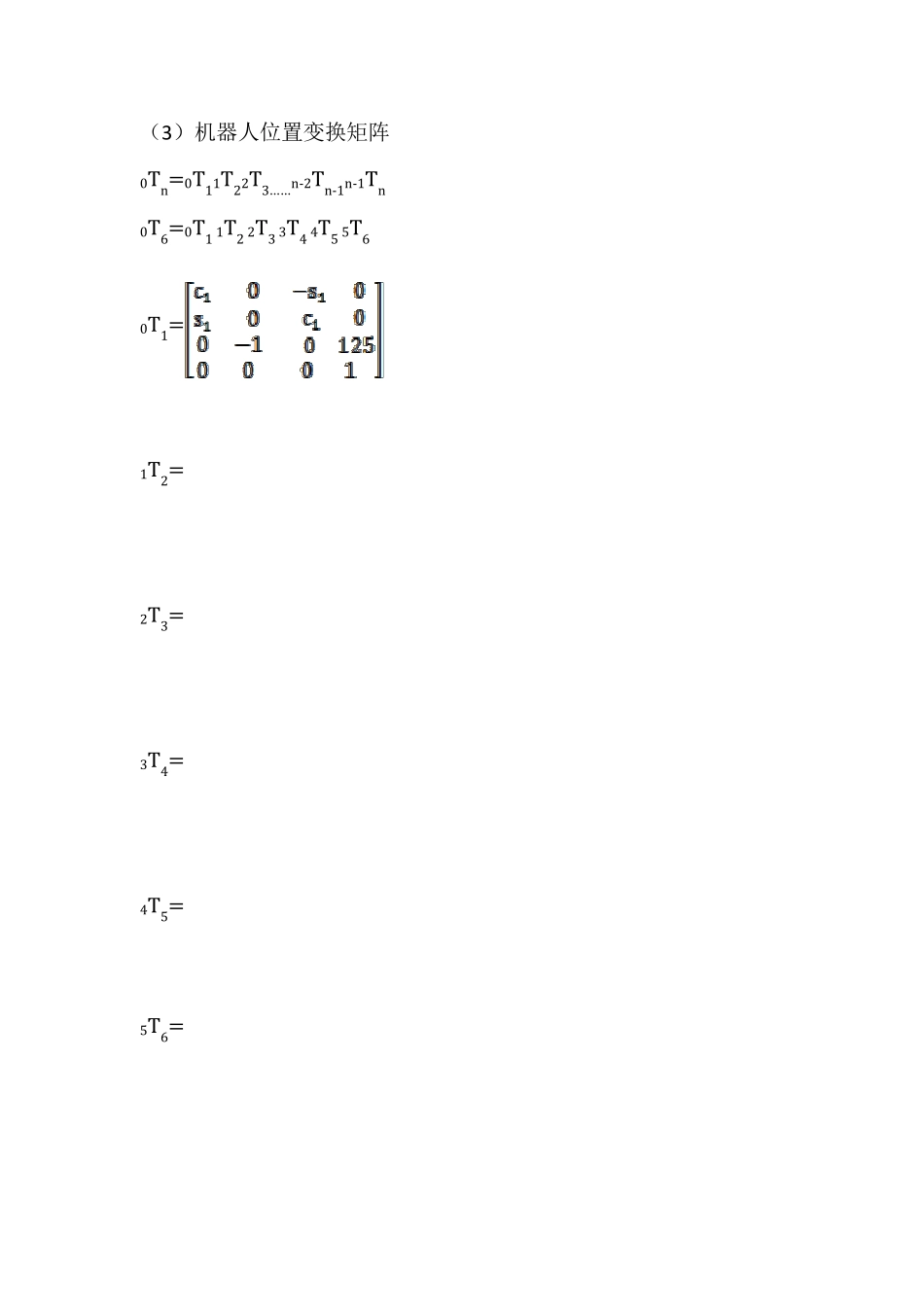Denso 垂直关节机器人的运动分析 一、 实验目的: 1. 理解串联机器人运动学的 D-H 坐标系的建立方法; 2. 掌握串联机器人的运动学方程的建立; 3. 会运用运动方程求解运动学的正解和反解。 二、 实验原理: 1. 机器人结构分析 (1)Denso 机器人齐次坐标系的建立(给出坐标系示意图) (2)Denso 机器人的杆件参数(参考指标参考实验一结构示意图) 变量 关节 d/mm a/mm 1 125 0 -90 2 0 210 0 3 0 75 -90 4 210 0 90 5 0 0 90 6 0 0 0 (3 )机器人位置变换矩阵 0Tn=0T11T22T3……n-2Tn-1n-1Tn 0T6=0T1 1T2 2T3 3T4 4T5 5T6 0T1= 1T2= 2T3= 3T4= 4T5= 5T6= 0T6= 其中: 式中 2.运动学正解 把相应的角度值代入以上各式便得到了运动学正解的变换矩阵。 3.运动逆解 现在已知机器人的末端位姿矩阵,求出各关节旋转的角度。 注意到 将上面两式相除得: , 由式0T6=0T1 1T2 2T3 3T4 4T5 5T6,得: 0T1-1 0T6= 1T2 2T3 3T4 4T5 5T6 取第一行第四列和第二行第四列得: 令,,移项得: 对上面两式左右两边同时平方然后相加得: 化简得: 同理,求第三个角: 令Q=1T2 -1 0T1-1 0T6 则: Q= 2T3 3T4 4T5 5T6 取第一行第四列得: 可以求得 令M=2T3-1 1T2 -1 0T1-1 0T6 则: M= 3T4 4T5 5T6 取第一行第三列,第三行第二列,第三行第三列得: 于是就求出了。 正解实验代码: PI=3.1415926; a=importdata('1.txt'); syms a1; syms a2; syms a3; syms a4; syms a5; syms a6; a1=a(1)/180*PI; a2=a(2)/180*PI; a3=a(3)/180*PI; a4=a(4)/180*PI; a5=a(5)/180*PI; a6=a(6)/180*PI; A1=[cos(a1) 0 -sin(a1) 0;sin(a1) 0 cos(a1) 0;0 -1 0 125;0 0 0 1]; A2=[cos(a2) -sin(a2) 0 210*cos(a2);sin(a2) cos(a2) 0 210*sin(a2);0 0 1 0;0 0 0 1]; A3=[cos(a3) 0 -sin(a3) 75*cos(a3);sin(a3) 0 cos(a3) 75*sin(a3);0 -1 0 0;0 0 0 1]; A4=[cos(a4) 0 sin(a4) 0;sin(a4) 0 -cos(a4) 0;0 1 0 210;0 0 0 1]; A5=[cos(a5) 0 sin(a5) 0;sin(a5) 0 -cos(a5) 0;0 1 0 0;0 0 0 1]; A6=[cos(a6) -sin(a6) 0 0;sin(a6) cos(a6) 0 0;0 0 1 0;0 0 0 1]; B=A1*A2*A3*A4*A5*A6 当输入目标角度:10 30 30 40 50 60 运行结果: 逆解实验代码: %%机器...