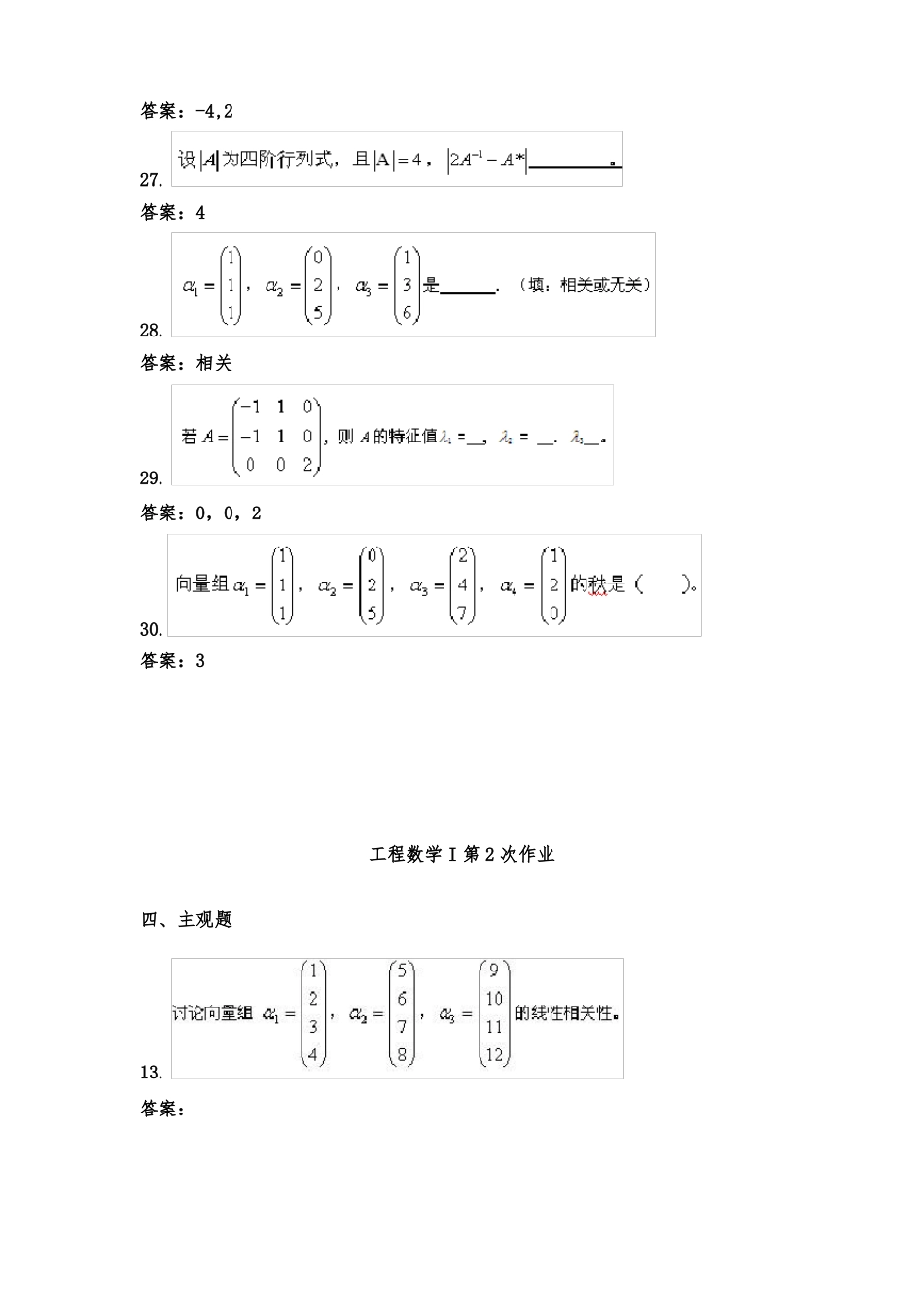
工程数学 I 第 1 次作业四、主观题22.答案:t=523.答案:2424、答案:-325.答案:26.答案:-4,227.答案:428.答案:相关29.答案:0,0,230.答案:3工程数学 I 第 2 次作业四、主观题13.答案:令,则A 的阶梯形有零行,所以向量组线性相关。14.求解齐次方程组答案:对方程组的系数矩阵作初等行变换化成简单阶梯形矩阵15.已知四元线性方程组答案:16.设,求 A 的特征值和特征向量。答案:17.求一个正交矩阵 P,将对称矩阵化为对角矩阵。答案:18.设二次型经过正交变换化为求参数 a、b 及所用的正交变换矩阵。答案:变换前后的两个二次型的矩阵分别为工程数学 I 第 4 次作业四、主观题13.计算行列式答案:容易发现 D 的特点是:每列(行)元素之和都等于 6,那么,把二、三、四行同时加到第一行,并提出第一行的公因子 6,便得到得由于上式右端行列式第一行的元素都等于 1,那么让二、三、四行都减去第一行14.求行列式答案:中元素 a 和 b 的代数余子式。行列式展开方法==15.设答案:,判断 A 是否可逆?若可逆,求出即所以16.求矩阵 X 使之满足答案:17.用初等行变换求矩阵答案:的逆矩阵于是同样道理,由算式可知,若对矩阵(A,B)施行初等行变换,当把 A 变为 E 时,B 就变为18.讨论向量组答案:,,的线性相关性。即19.用正交变换把二次型化为标准型。答案:二次型的矩阵正交化得位化得工程数学 I 第 5 次作业四、主观题14.答案:15.答案:16.答案:17.答案:18.计算四阶行列式答案:将行列式 D 按第三行展开得19.求方程组的一个基础解系并求其通解。答案:对方程组的系数矩阵作初等行变换化成简单阶梯形矩阵:原方程组的一个基础解系。20.a、b 为何值时,线性方程组有唯一解,无解或有无穷多解?在有无穷多解时,求其通解?答案: