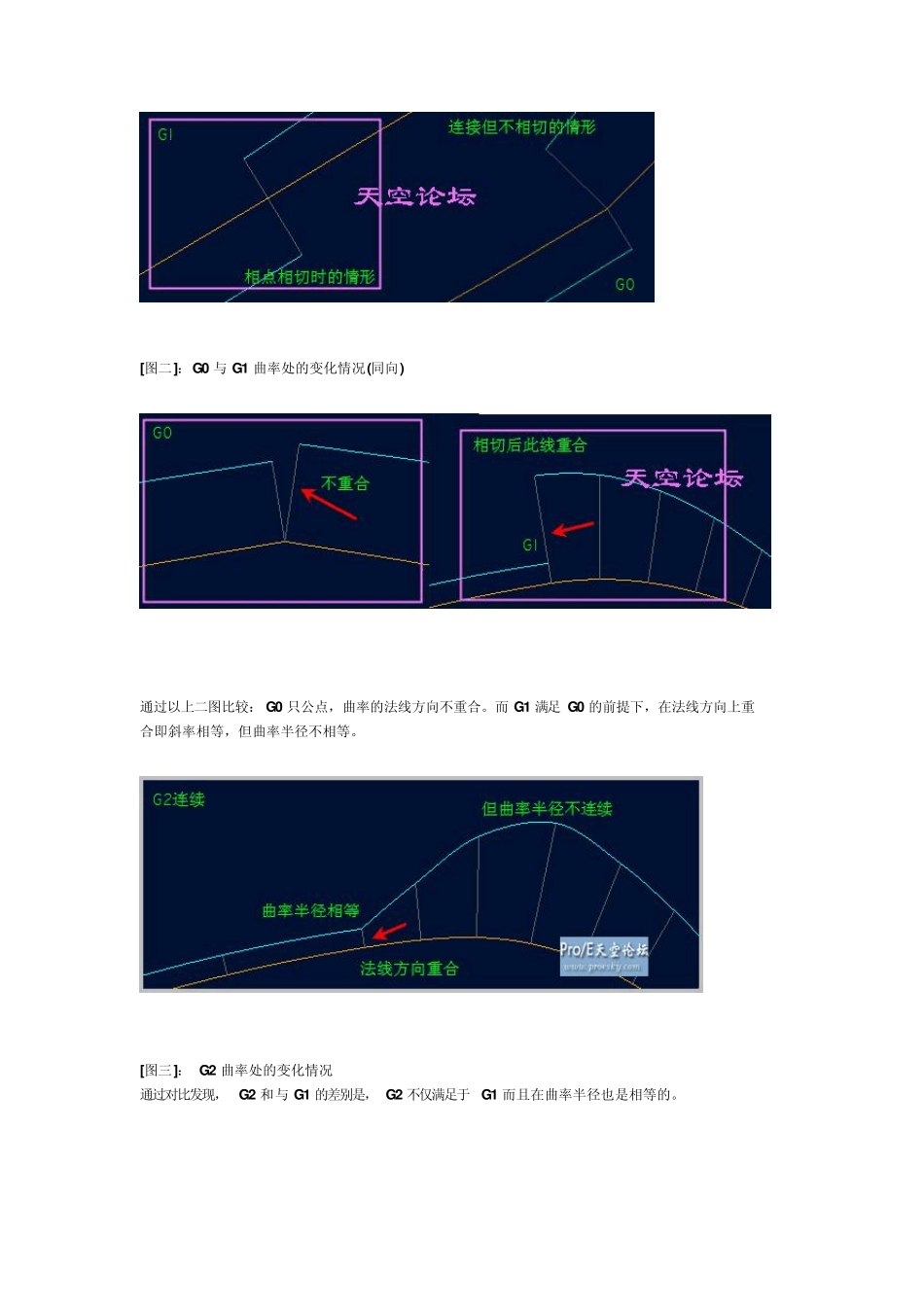
[前言]:本教程主要详述曲面的曲率连的问题,在曲面设计过程,往往要追求高质量的曲面。这就需要我们对曲率的问题进行探讨,通过正确的方法和技巧去达到高质量的曲面。首先要明确一点,要达到一个高质量的曲面,那么同时也要有高质量的曲线作为架构,才能构造出符合设计意向的曲面。 下面首先讲解一下曲率的几何连续性的概念和印象,我们可以简单的做个理解,学术定义相对抽象。 G0--几何共用一条公共边界或一个点。在相切(斜率)和曲率连续性(斜率改变)两个方面均不连续。 G1--斜率连续。几何连接而且相切(斜率连续),但曲率不连续。 G2--曲率连续。几何连接、相切且曲率连续。 G3--曲率变化率连续 这种连续级别不仅具有上述连续级别的特征之外,在接点处曲率的变化率也是连续的,这使得曲率的变化更加平滑。曲率的变化率可以用一个一次方程表示为一条直线。 这种连续级别的表面有比 G2 更流畅的视觉效果。但是由于需要用到高阶曲线或需要更多的曲线片断所以通常只用于汽车设计。 G4--曲率变化率的变化率连续 “变化率的变化率”似乎听起来比较深奥,实际上可以这样理解,它使曲率的变化率开始缓慢,然后加快,然后再慢慢的结束。这使得 G4 连续级别能够提供更加平滑的连续效果。 但是这种连续级别将比 G3 计算起来更复杂,所以几乎不会在小家电一类的产品设计中出现。实际上,就算出现了,我们也未必看得出来。 本节主要讲解曲率的前三种情况:G0、G1、G2 连续。关于 G3、G4 只做了解。下面通过图片说明曲线和曲面的曲率连续情况,使抽象化的概念更加形象化一些。 一、曲线的曲率控制。 1、曲线中的G0、G1、G2 连续情况。 [图一]曲线的G0 连续 [图二]:G0 与 G1 曲率处的变化情况(反向) [图二]:G0 与G1 曲率处的变化情况(同向) 通过以上二图比较:G0 只公点,曲率的法线方向不重合。而 G1 满足 G0 的前提下,在法线方向上重合即斜率相等,但曲率半径不相等。 [图三]: G2 曲率处的变化情况 通过对比发现,G2 和与G1 的差别是,G2 不仅满足于 G1 而且在曲率半径也是相等的。 [图四]: G3 曲率连续情况 由图可以看出,G3 满足G2 的条件且曲率的变化率也接近连续。关于G3 连续只有通过调整各曲线的曲率进行优化,才能达到在接点处曲率连续。 [ 此贴被meiyucd 在2007-07-07 18:14 重新编辑 ] 清空我的评分动态本帖最近评分记录: 共1 条评分记录 abolou 威望 +2 ...