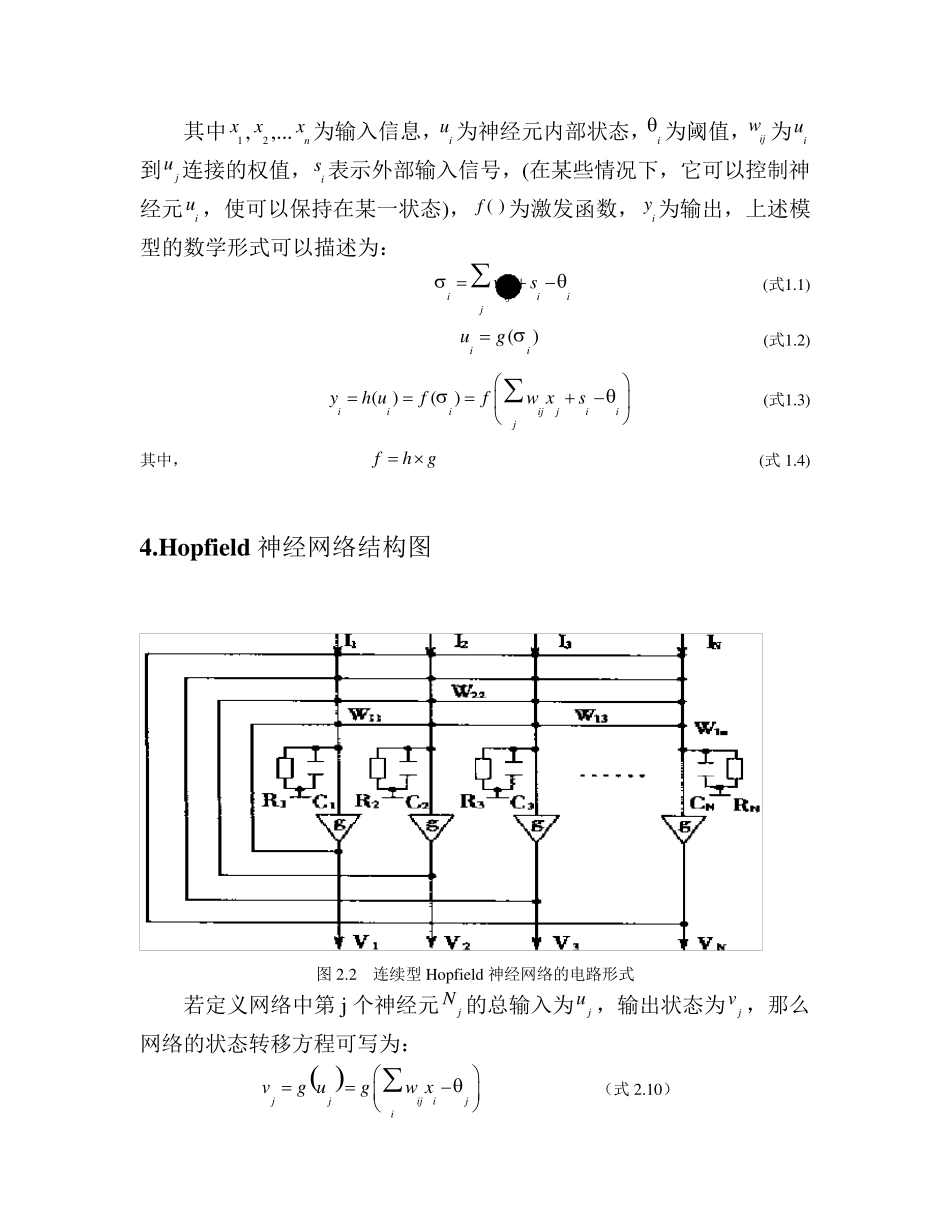
Hopfield 神经网络求解TSP 问题 1.什么是TSP 问题? 旅行商问题,即TSP 问题(Traveling Salesman Problem),也是最优化问题。一个旅行商人要拜访n 个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要 回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。 用数学语言描述TSP 如下 :设有限个城市集合 : C = { C1 , C 2 , … , Cn },每两个城市间的距离为 d(Ci,Cj)∈Z, 其中 Ci,Cj∈C( 1<=i , j <=n), 即求 minL=∑d(Ci,Cj)的值的问题。 有效 路径的方 案 数目为Rn= ((n-1 )! /2 ), 例如:R4=3,R5=12,R6=120,R10=181440 可见路径总数,随 n 增大而急剧增长,当城市数目增加到一定的程度,计算量增加到无法进行的地步,所以要选择一种合理快速的算法,而不能对所有情况使用人工列举的方法。 2.Hopfield 神经网络介绍 人工神经网络(Artificial Neural Networks,简写为ANNs)也简称为神经网络(NNs)或称作连接模型(Connection Model),它是一种模仿动物神经网络行为特征,进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度,通过调整内部大量节点之间相互连接的关系,从而达到处理信息的目的.最基础的为BP、Hopfield 网络等。 Hopfield 网络是一种互连型网络的一种,它引入类似于 Lyapunov函数的能量函数概念,把神经网络的拓扑结构(用连接权矩阵表示)与所求问题(用目标函数描述)相对应,并将其转换为神经网动力学系统的演化问题。 3 .神经元的数学模型 人的大脑是由大量神经细胞或神经元组成的。每个神经元可以看作为一个小的处理单元,这些神经元按照某种方式相互连接起来,构成大脑内部的生理神经元网络系统,他们中各个神经元之间连接的强弱不是固定不变的,而是按照外部的信号激励程度做自适应的变化,而每个神经元又随着接收到的多个激励信号的综合大小呈现兴奋或抑制状态。大脑的学习过程就是神经元之间连接强度随外部激励信号做自适应变化的过程。大脑处理信息的结果由神经元状态表现出来。由此见,神经元是信息处理的最小单位。神经元,也就是神经细胞,由细胞体、树突、轴突和突触组成。从细胞体上伸出许多树突和一条长的轴突,树突和轴突分别负责传入和传出兴奋或抑制信号到细胞体。神经元的树突短而且分支很多,是信号的输入端;轴突较长,是信号的输出端,其未端化为许多细小的分...