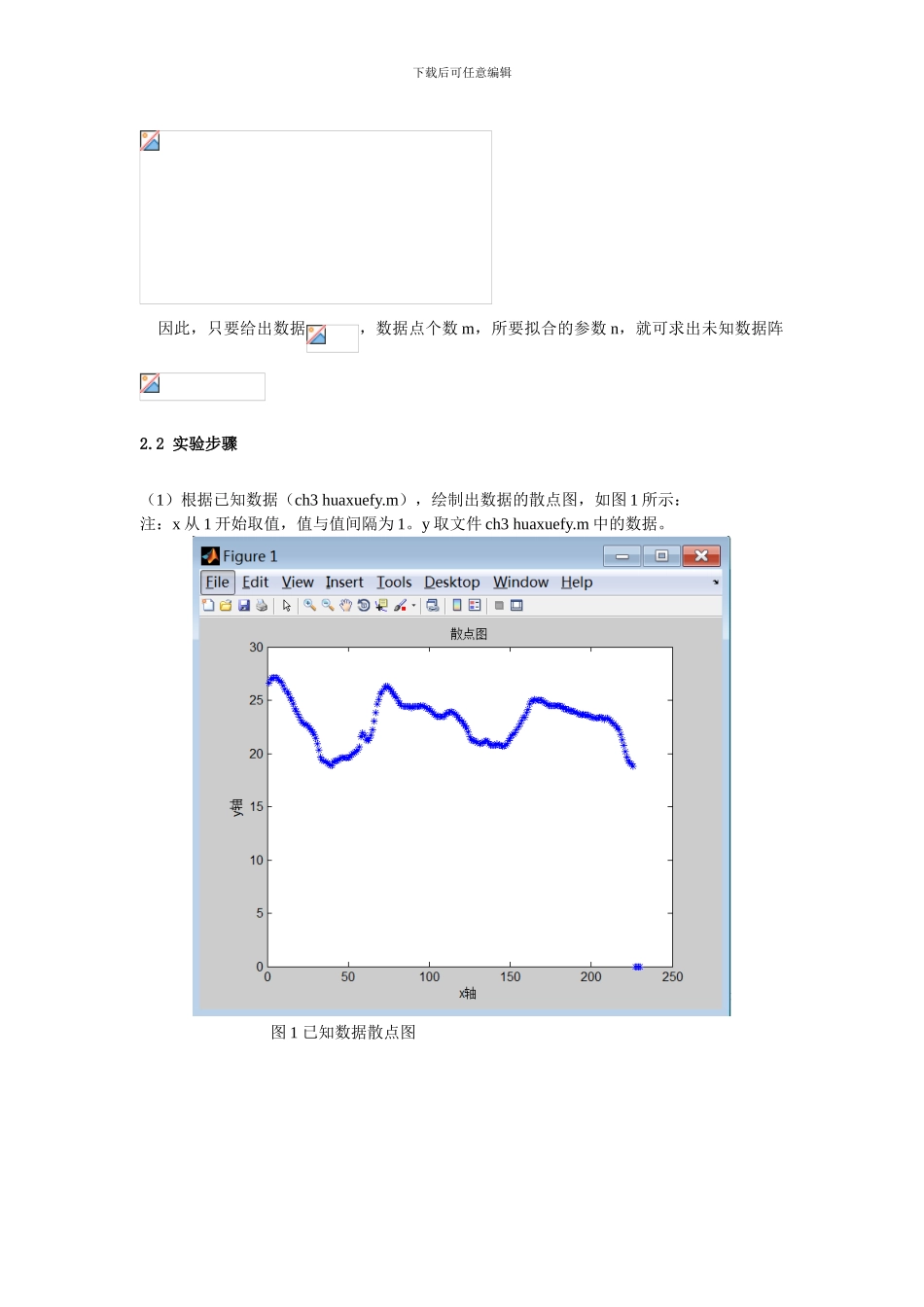
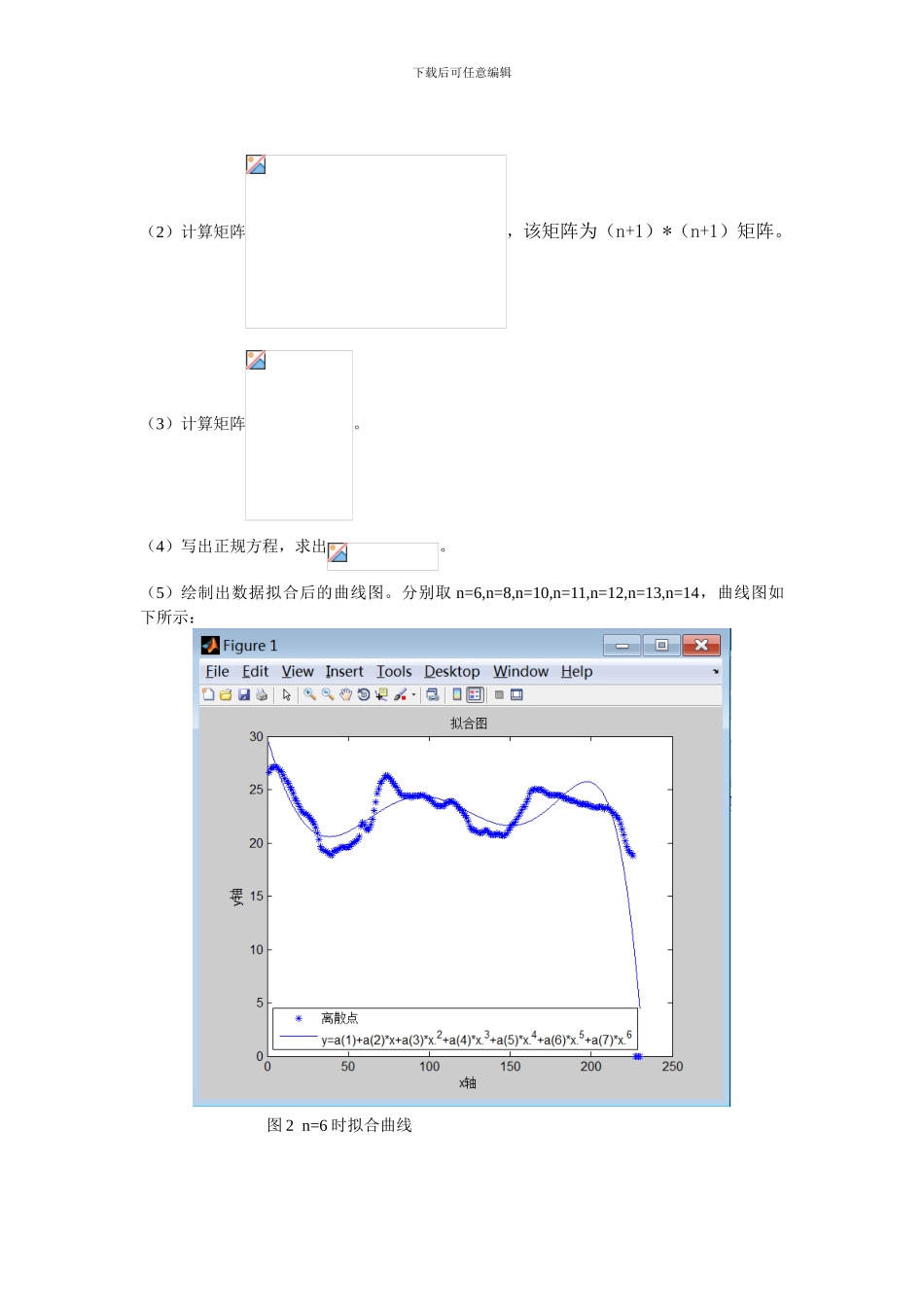
下载后可任意编辑实验题目: 用多项式模型进行数据拟合 实验 1 实验目的本实验使用多项式模型对数据进行拟合,目的在于:(1)掌握数据拟合的基本原理,学会使用数学的方法来判定数据拟合的情况;(2)掌握最小二乘法的基本原理及计算方法;(3)熟悉使用 matlab 进行算法的实现。2 实验步骤2.1 算法原理 所谓拟合是指寻找一条平滑的曲线,最不失真地去表现测量数据。反过来说,对测量的实验数据,要对其进行公式化处理,用计算方法构造函数来近似表达数据的函数关系。由于函数构造方法的不同,有许多的逼近方法,工程中常用最小平方逼近(最小二乘法理论)来实现曲线的拟合。 最小二乘拟合利用已知的数据得出一条直线或曲线,使之在坐标系上与已知数据之间的距离的平方和最小。模型主要有:1.直线型 2.多项式型 3.分数函数型 4.指数函数型 5.对数线性型 6.高斯函数型等,根据应用情况,选用不同的拟合模型。其中多项式型拟合模型应用比较广泛。 给定一组测量数据,其中,共 m+1 个数据点,取多项式P(x),使得,则称函数 P(x)为拟合函数或最小二乘解,此时,令,使得,其中为 待 求 的 未 知 数 , n 为 多 项 式 的 最 高 次 幂 , 由 此 该 问 题 化 为 求的极值问题。由 多 元 函 数 求 极 值 的 必 要 条 件 :, 其 中得到:,其中,这是一个关于的线性方程组,用矩阵表示如下所示:下载后可任意编辑 因此,只要给出数据,数据点个数 m,所要拟合的参数 n,就可求出未知数据阵2.2 实验步骤(1)根据已知数据(ch3 huaxuefy.m),绘制出数据的散点图,如图 1 所示:注:x 从 1 开始取值,值与值间隔为 1。y 取文件 ch3 huaxuefy.m 中的数据。 图 1 已知数据散点图下载后可任意编辑(2)计算矩阵,该矩阵为(n+1)*(n+1)矩阵。(3)计算矩阵。(4)写出正规方程,求出。(5)绘制出数据拟合后的曲线图。分别取 n=6,n=8,n=10,n=11,n=12,n=13,n=14,曲线图如下所示: 图 2 n=6 时拟合曲线下载后可任意编辑 图 3 n=8 时拟合曲线 图 4 n=10 时拟合曲线下载后可任意编辑 图 5 n=11 时拟合曲线 图 6 n=12 时拟合曲线下载后可任意编辑 图 7 n=13 时拟合曲线 3 实验结果分析通过运用最小二乘法对多项式模型进行数据拟合处理,获得 n 次多项式及其系数。分别取多项式次数 n=6,n=8,n=10,n=11,n=12,n=13,n=14 绘制拟合曲线,观察曲线...