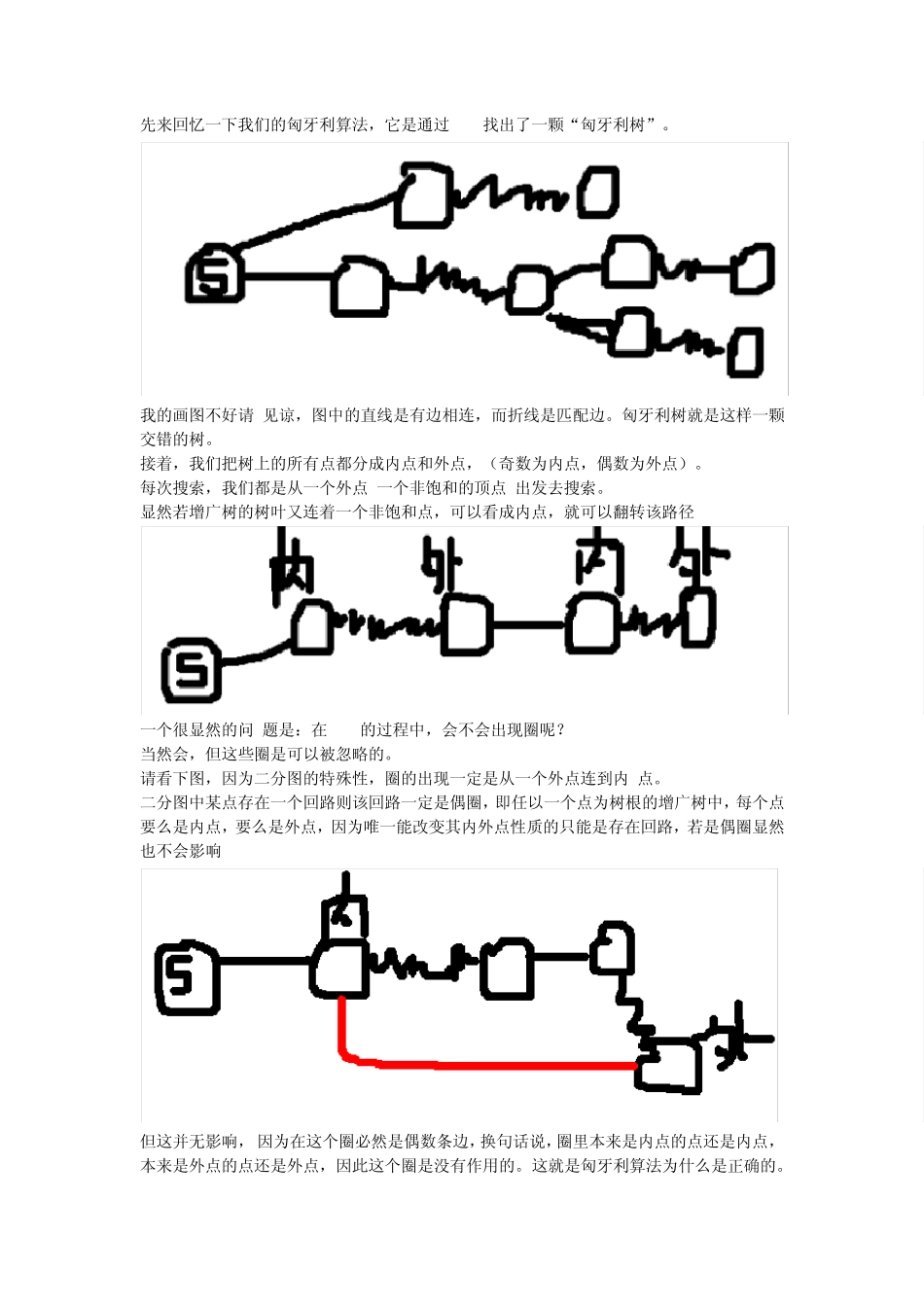
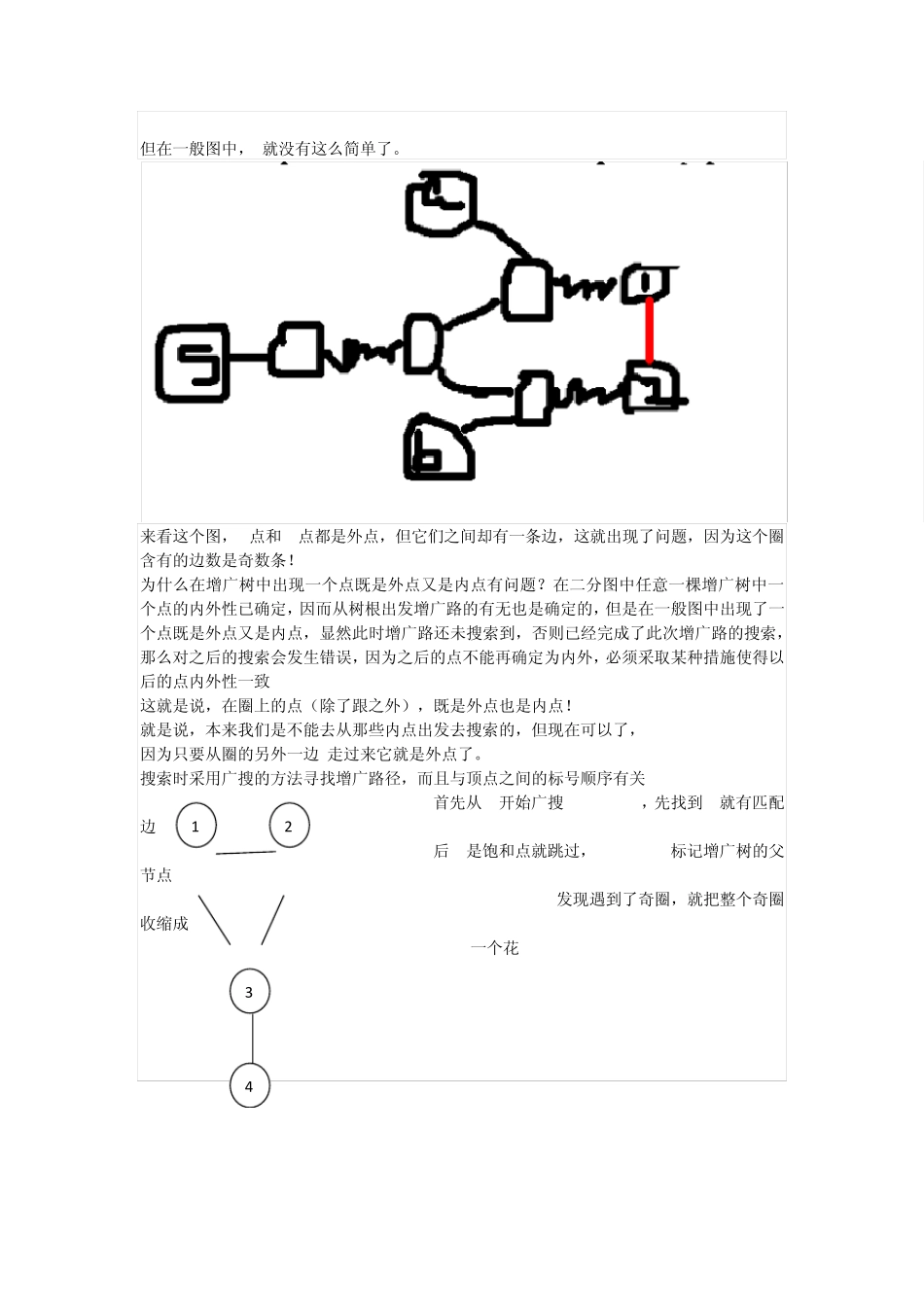
先来回忆一下我们的匈牙利算法,它是通过DFS找出了一颗“匈牙利树”。 我的画图不好请 见谅,图中的直线是有边相连,而折线是匹配边。匈牙利树就是这样一颗交错的树。 接着,我们把树上的所有点都分成内点和外点,(奇数为内点,偶数为外点)。 每次搜索,我们都是从一个外点(一个非饱和的顶点)出发去搜索。 显然若增广树的树叶又连着一个非饱和点,可以看成内点,就可以翻转该路径 一个很显然的问 题是:在 DFS的过程中,会不会出现圈呢? 当然会,但这些圈是可以被忽略的。 请看下图,因为二分图的特殊性,圈的出现一定是从一个外点连到内 点。 二分图中某点存在一个回路则该回路一定是偶圈,即任以一个点为树根的增广树中,每个点要么是内点,要么是外点,因为唯一能改变其内外点性质的只能是存在回路,若是偶圈显然也不会影响 但这并无影响, 因为在这个圈必然是偶数条边,换句话说,圈里本来是内点的点还是内点, 本来是外点的点还是外点,因此这个圈是没有作用的。这就是匈牙利算法为什么是正确的。 但在一般图中, 就没有这么简单了。 来看这个图,1点和 2点都是外点,但它们之间却有一条边,这就出现了问题,因为这个圈含有的边数是奇数条! 为什么在增广树中出现一个点既是外点又是内点有问题?在二分图中任意一棵增广树中一个点的内外性已确定,因而从树根出发增广路的有无也是确定的,但是在一般图中出现了一个点既是外点又是内点,显然此时增广路还未搜索到,否则已经完成了此次增广路的搜索,那么对之后的搜索会发生错误,因为之后的点不能再确定为内外,必须采取某种措施使得以后的点内外性一致 这就是说,在圈上的点(除了跟之外),既是外点也是内点! 就是说,本来我们是不能去从那些内点出发去搜索的,但现在可以了, 因为只要从圈的另外一边 走过来它就是外点了。 搜索时采用广搜的方法寻找增广路径,而且与顶点之间的标号顺序有关 首先从 1开始广搜 1->2,1->3,先找到 2就有匹配边 1-2 后 2是饱和点就跳过,3->1,3->2标记增广树的父节点 3->1->2发现遇到了奇圈,就把整个奇圈收缩成 一个花 1 3 2 4 所谓的带花树算法就是,把整个圈缩成一个点,Edmonds称这个超级点为“花”, 就是说,原圈里的所有点都作为外点,然后继续搜索。再之后的过程中,已经被缩的点还可能被嵌套地收缩。 当我们找到一条增广路之后,还要把路上的“花”展开。 总之,带花树的算法思想就是缩点-继续找增广路...