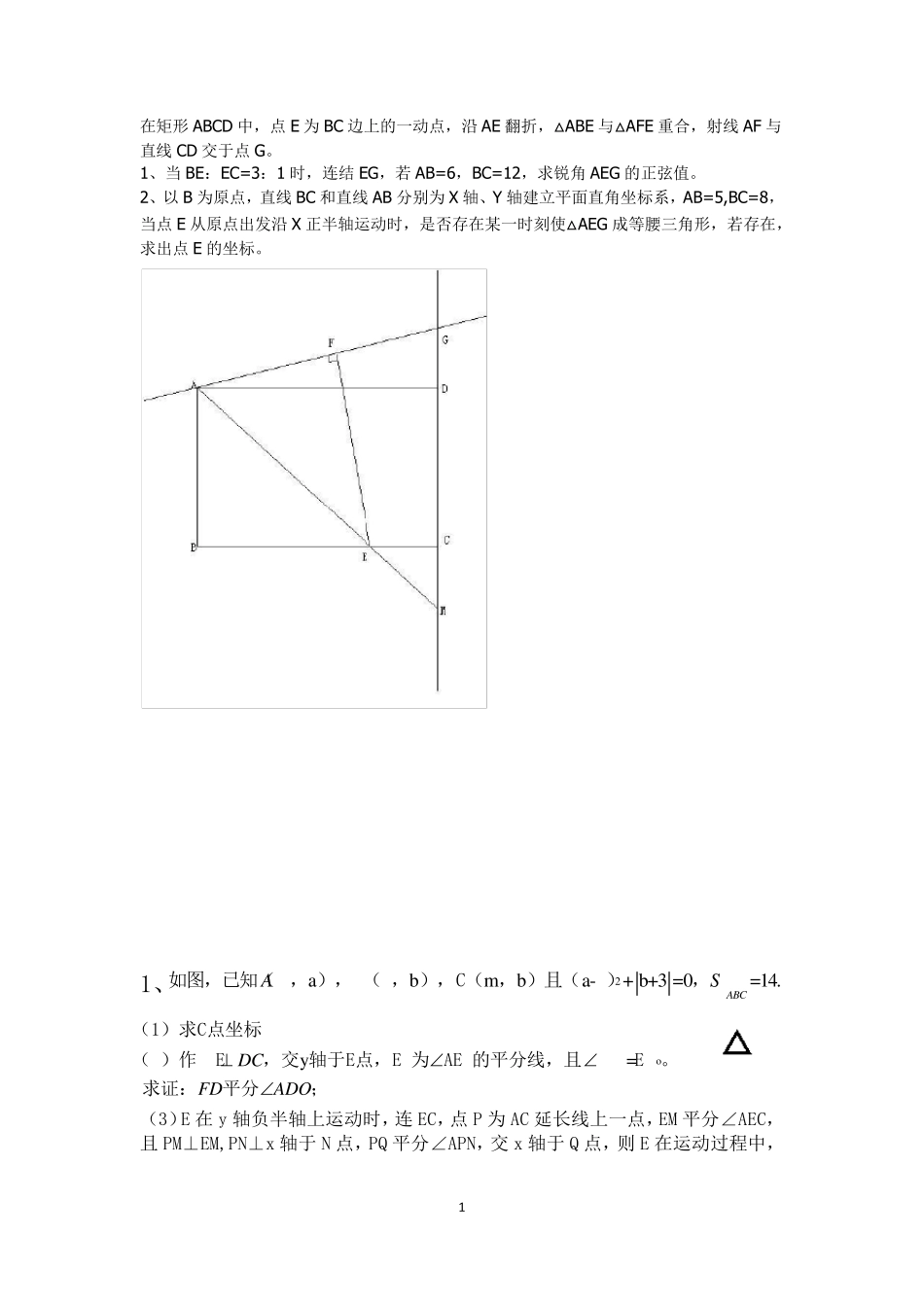
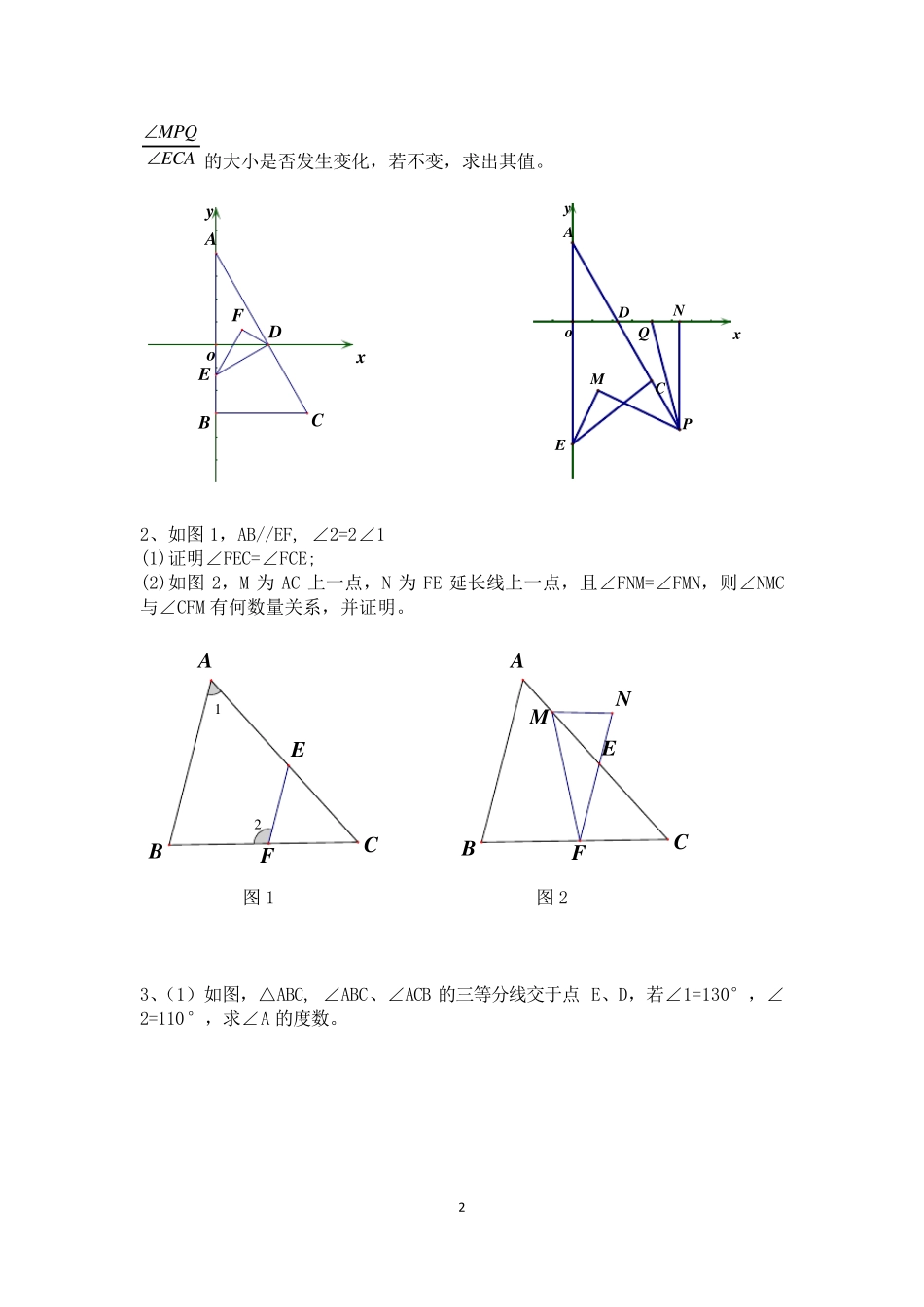
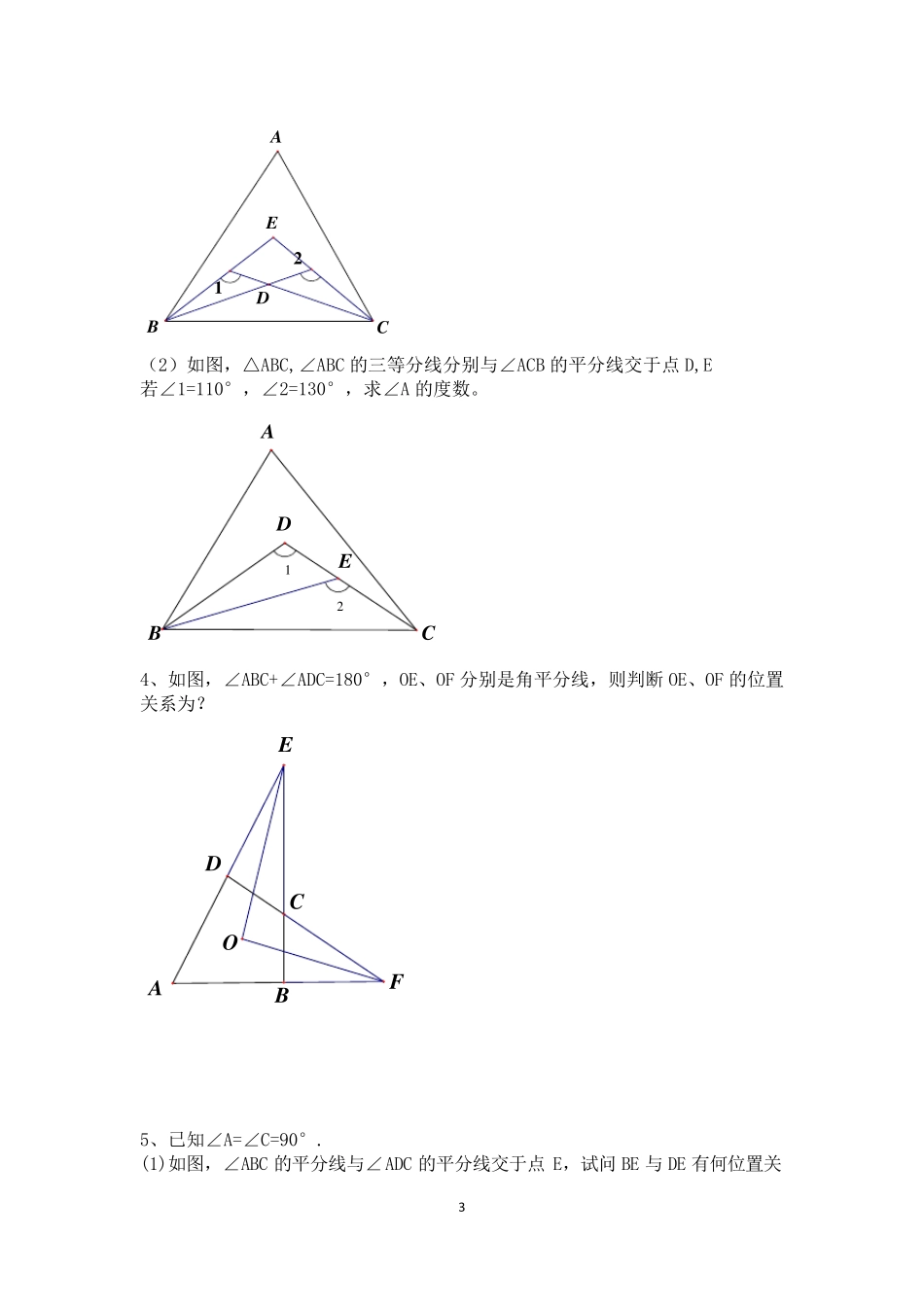
1 在矩形ABCD 中,点E 为BC 边上的一动点,沿AE 翻折,△ABE 与△AFE 重合,射线AF 与直线CD 交于点G。 1、当BE:EC=3:1 时,连结EG,若AB=6,BC=12,求锐角AEG 的正弦值。 2、以B 为原点,直线BC 和直线AB 分别为X 轴、Y 轴建立平面直角坐标系,AB=5,BC=8,当点E 从原点出发沿X 正半轴运动时,是否存在某一时刻使△AEG 成等腰三角形,若存在,求出点E 的坐标。 1、2abmba-+ b+3 =0=14.ABCAS如图,已知(0,),B(0,),C(,)且(4) , oy=DCFDADO(1)求C点坐标(2)作DE,交轴于E点,EF为AED的平分线,且DFE90。求证:平分; (3)E 在y 轴负半轴上运动时,连EC,点P 为AC 延长线上一点,EM 平分∠AEC,且PM⊥EM,PN⊥x 轴于N 点,PQ 平分∠APN,交x 轴于Q 点,则 E 在运动过程中,2 MPQECA的大小是否发生变化,若不变,求出其值。 2、如图1,AB//EF, ∠2=2∠1 (1)证明∠FEC=∠FCE; (2)如图2,M 为AC 上一点,N 为FE 延长线上一点,且∠FNM=∠FMN,则∠NMC与∠CFM 有何数量关系,并证明。 图1 图2 3、(1)如图,△ABC, ∠ABC、∠ACB 的三等分线交于点E、D,若∠1=130°,∠2=110°,求∠A 的度数。 xyFDCBAoExyQNMDCAoPE21EABCFNEABCFM3 (2)如图,△ABC,∠ABC 的三等分线分别与∠ACB 的平分线交于点D,E 若∠1=110°,∠2=130°,求∠A 的度数。 4、如图,∠ABC+∠ADC=180°,OE、OF 分别是角平分线,则判断 OE、OF 的位置关系为? 5、已知∠A=∠C=90°. (1)如图,∠ABC 的平分线与∠ADC 的平分线交于点E,试问 BE 与DE 有何位置关21DABCE21ABCDEOFEDABC4 系?说明你的理由。 (2)如图,试问∠ABC 的平分线BE 与∠ADC 的外角平分线DF 有何位置关系?说明你的理由。 (3)如图,若∠ABC 的外角平分线与∠ADC 的外角平分线交于点E,试问BE 与DE 有何位置关系?说明你的理由。 6.(1)如图,点E 在AC 的延长线上,∠BAC 与∠DCE 的平分线交于点F,∠B=60°,∠F=56°,求∠BDC 的度数。 (2)如图,点E 在CD 的延长线上,∠BAD 与∠ADE 的平分线交于点F,试问∠F、∠B 和∠C 之间有何数量关系?为什么? 7.已知∠ABC 与∠ADC 的平分线交于点E。 (1)如图,试探究∠E、∠A 与∠C 之间的数量关系,并说明理由。 FAEBDCFCEBADECBADECBADGFECBADMN5 (2)如图,是探究∠E、∠A 与∠C 之间的数量关系,并说明理由。 8...