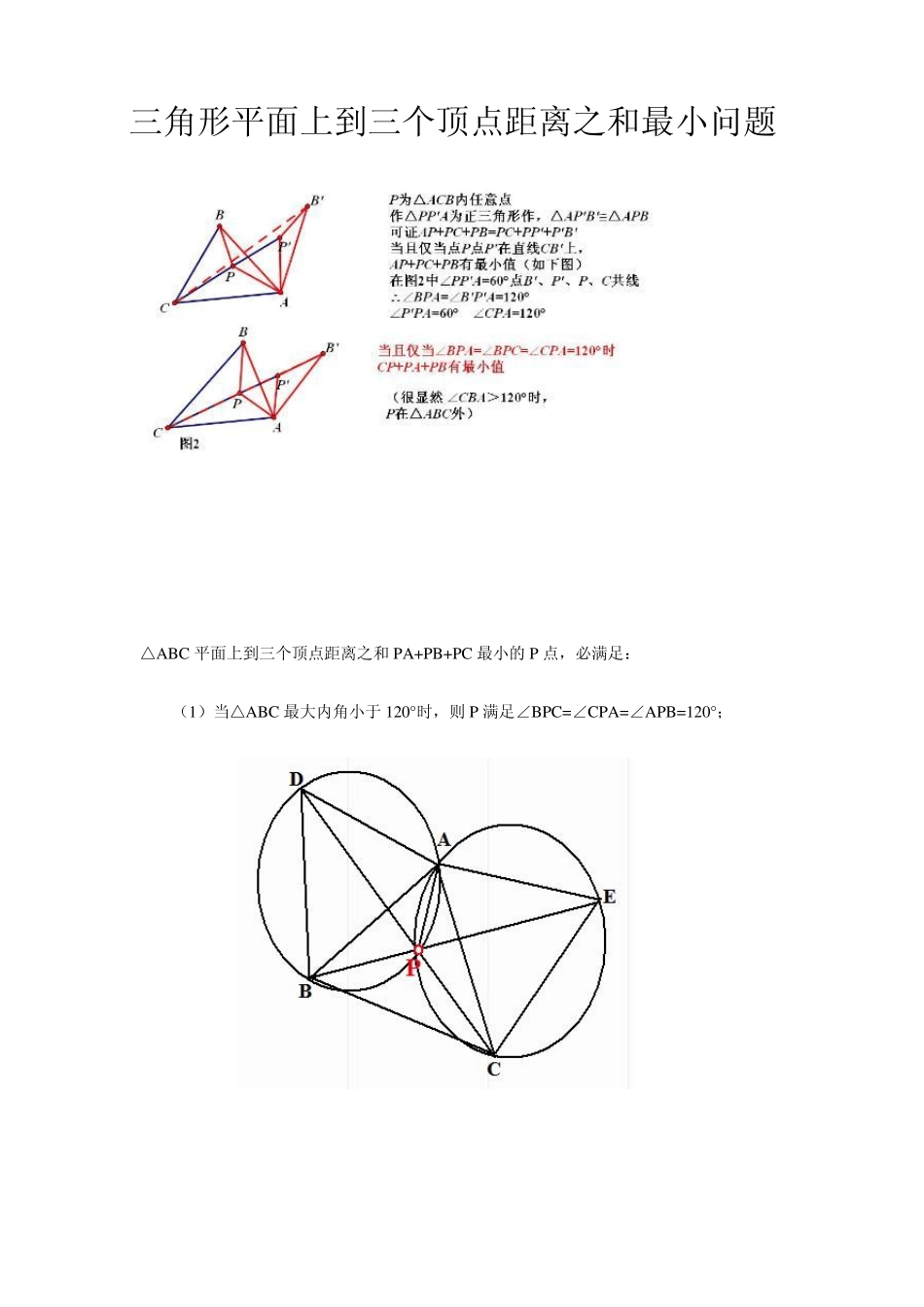
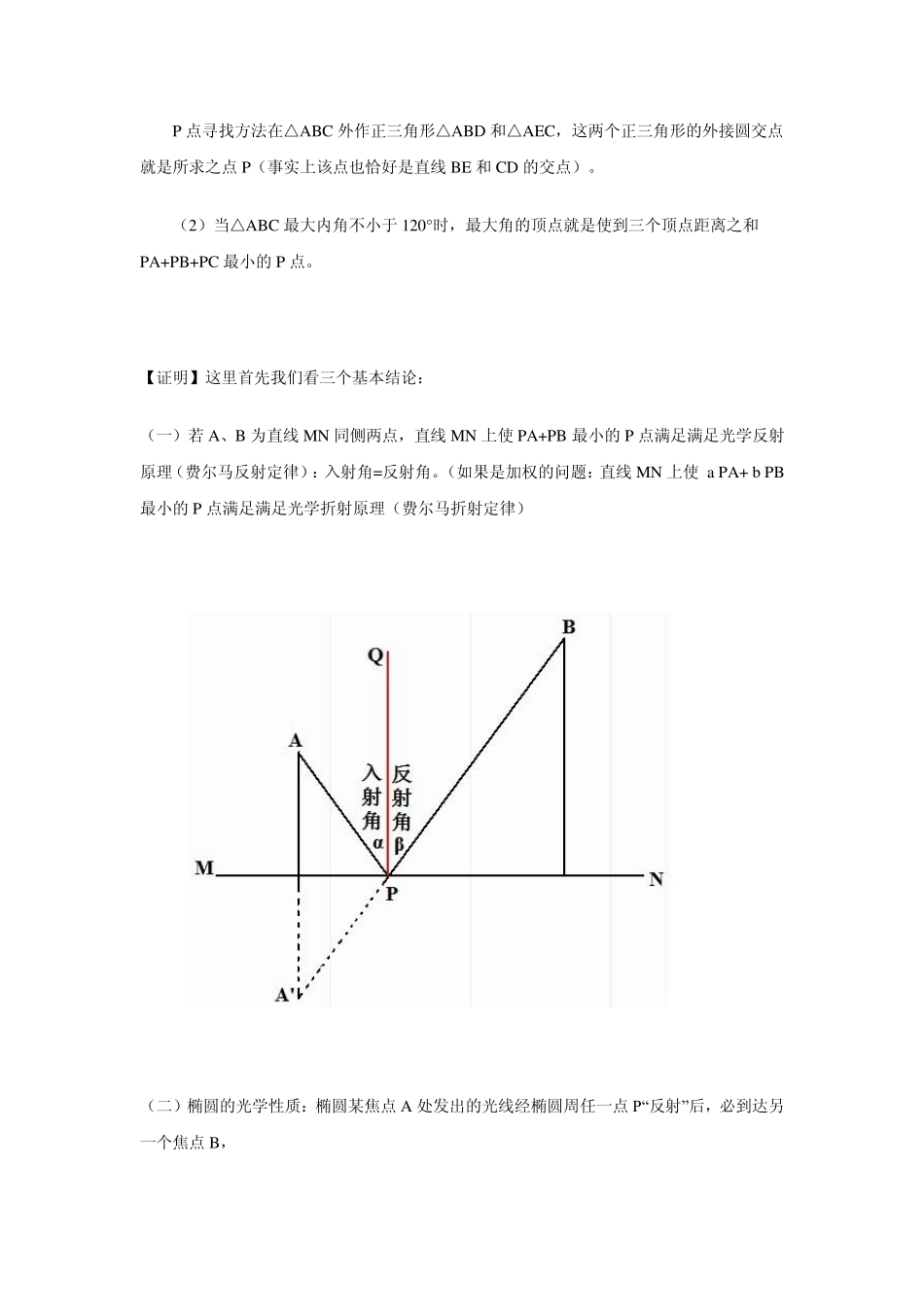
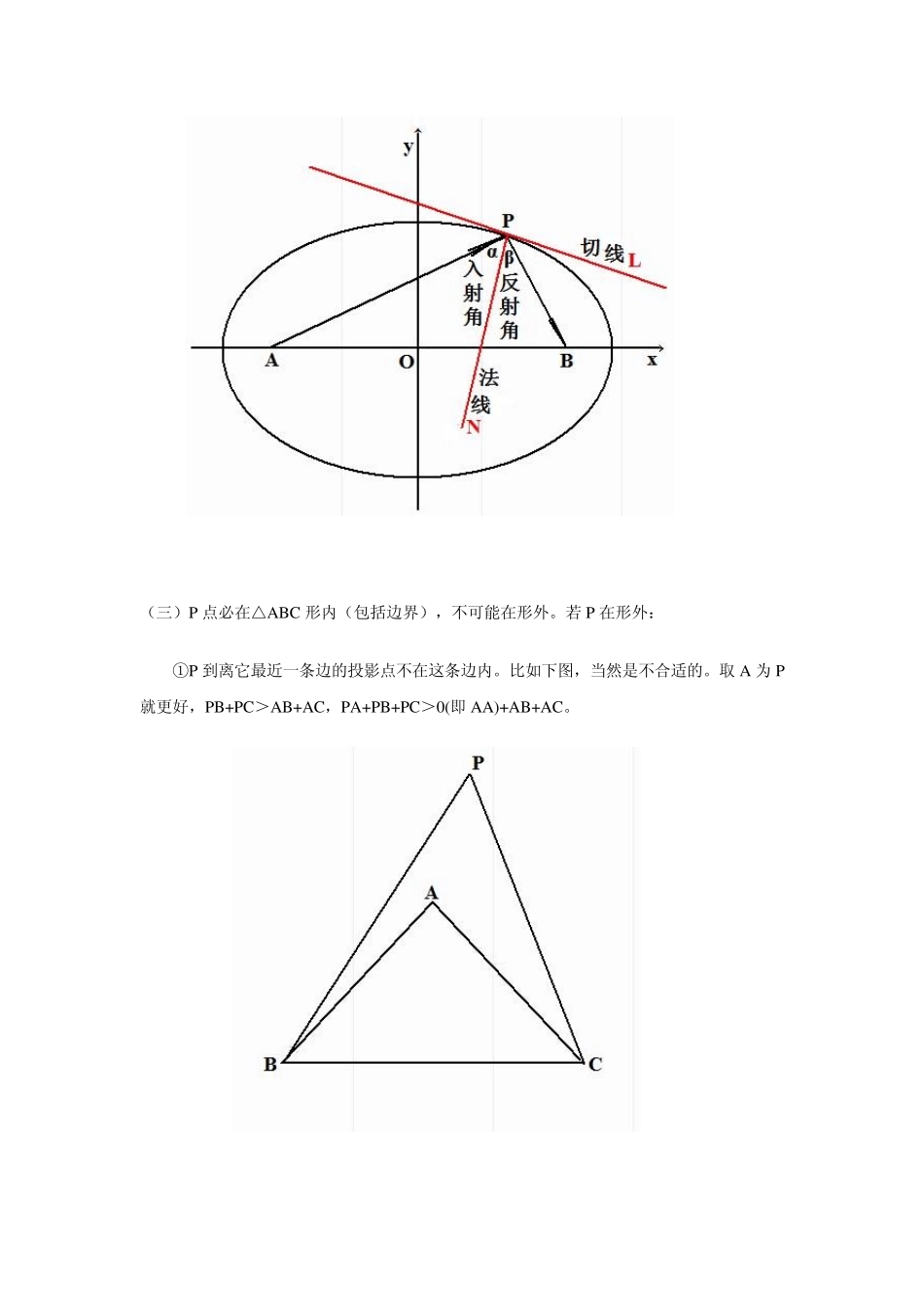
三角形平面上到三个顶点距离之和最小问题 △ABC 平面上到三个顶点距离之和PA+PB+PC 最小的P 点,必满足: (1)当△ABC 最大内角小于120°时,则P 满足∠BPC=∠CPA=∠APB=120°; P 点寻找方法在△ABC 外作正三角形△ABD 和△AEC,这两个正三角形的外接圆交点就是所求之点P(事实上该点也恰好是直线 BE 和 CD 的交点)。 (2)当△ABC 最大内角不小于 120°时,最大角的顶点就是使到三个顶点距离之和PA+PB+PC 最小的 P 点。 【证明】这里首先我们看三个基本结论: (一)若 A、B 为直线 MN 同侧两点,直线 MN 上使 PA+PB 最小的 P 点满足满足光学反射原理(费尔马反射定律):入射角=反射角。(如果是加权的问题:直线 MN 上使 a PA+ b PB 最小的 P 点满足满足光学折射原理(费尔马折射定律) (二)椭圆的光学性质:椭圆某焦点A 处发出的光线经椭圆周任一点P“反射”后,必到达另一个焦点B, (三)P点必在△ABC 形内(包括边界),不可能在形外。若P在形外: ①P到离它最近一条边的投影点不在这条边内。比如下图,当然是不合适的。取 A 为 P就更好,PB+PC>AB+AC,PA+PB+PC>0(即 AA)+AB+AC。 ②P 到离它最近一条边的投影点在这条边上(可以是端点),例如下图P 在AB 上的投影P'在AB 上,则 PA>P'A,PB+PC>P'B+P'C ⇒ PA+PB+PC>P'A+P'B+P'C。 现在,着手证明。 (1)假如△ABC 最大内角小于120°,为证明∠BPC=∠CPA=∠APB=120°,我们就先来证明 ∠APB=∠APC。 当 PB+PC 值确定时,P 点在以B、C 为焦点的椭圆上,在椭圆上使 PA 最小的P点应该使 PA 垂直于椭圆在P 点处的切线 MN(即:就是圆 A 与椭圆相切于P),根据椭圆的光学性质,必有∠APB=∠APC。(更充分的理由是反证法,任取另一点P2,显然 AP<AP2,而 PB+PC=P2B+P2C,所以PA+PB+PC<P2A+P2B+P2C) 或者在PA 为定值时,P 点在以A 为圆心的圆上,为使PB+PC 最小,P 必然在以B、C为焦点且与圆A 相切的椭圆上,则∠APB=∠APC。否则在圆A 上任取另一点P1,显然P1B+P1C>QB+QC=PB+PC,由于 P1A=PA,所以 P1A+P1B+P1C>PA+PB+PC。 (2)当△ABC 最大内角不小于 120°时,因为有前述理由,点P 不可能在△ABC 的形外。但是最大内角不小于 120°,例如∠A≥120°,那么△ABC 的形内的P 点,都有∠BPC>∠A,即∠BPC>120°, 所以满足∠BPC=∠CPA=∠APB=120°也不存在。 P 点既不在形外,也不在形内,那么只能在边界上,易知最大角的顶点,就是使PA+PB+PC 最小的 P 点位置的最佳选择。