三次函数性质大全

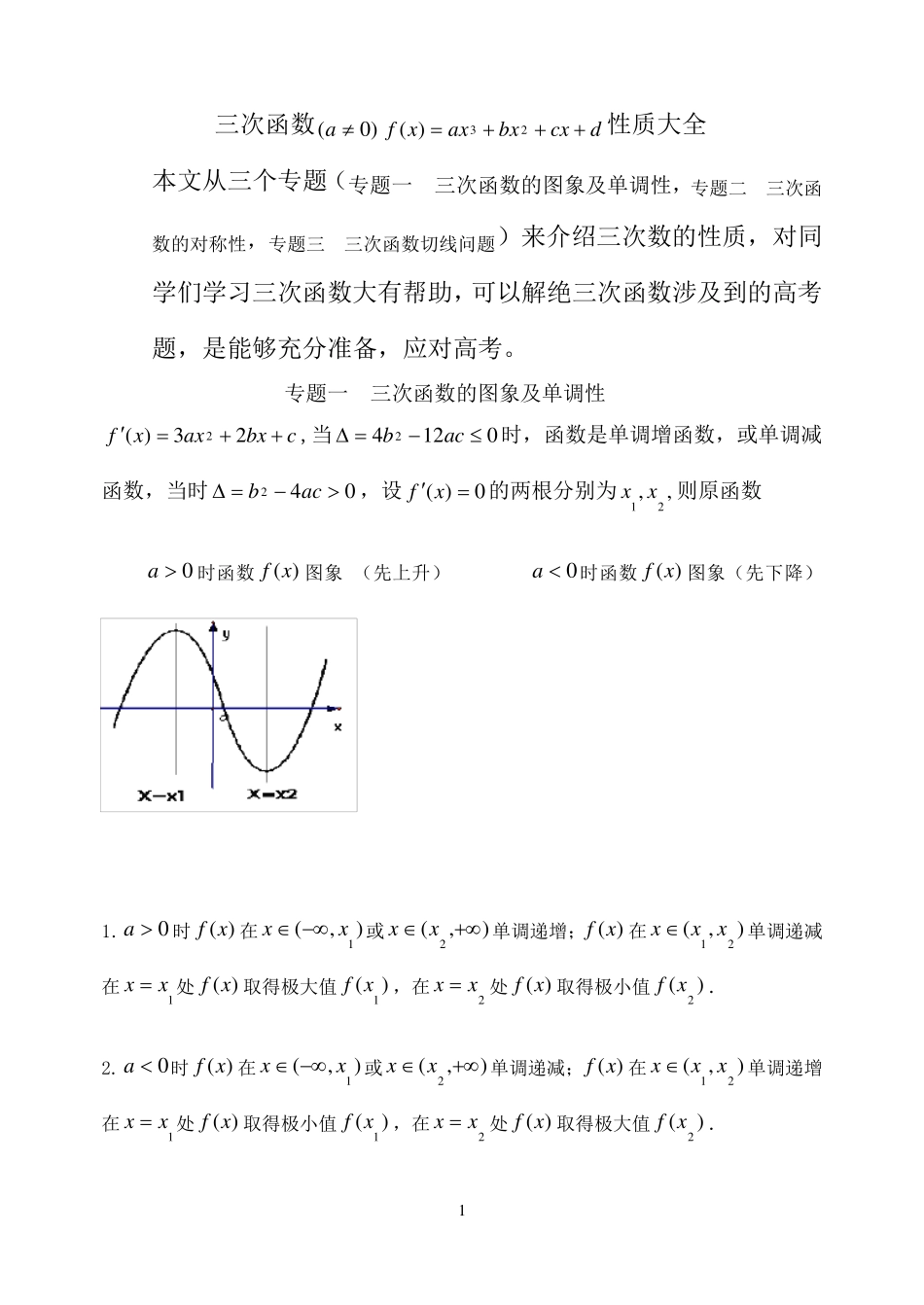
1 三次函数)0(adcxbxaxxf23)(性质大全 本文从三个专题（专题一 三次函数的图象及单调性，专题二 三次函数的对称性，专题三 三次函数切线问题）来介绍三次数的性质，对同学们学习三次函数大有帮助，可以解绝三次函数涉及到的高考题，是能够充分准备，应对高考。 专题一 三次函数的图象及单调性 cbxaxxf23)(2,当01 242acb时，函数是单调增函数，或单调减函数，当时042acb，设0)( xf的两根分别为,,21 xx则原函数 0a时函数)(xf图象 （先上升） 0a时函数)(xf图象（先下降） 1.0a时)(xf在),(1xx或),(2  xx单调递增；)(xf在),(21 xxx 单调递减在1xx 处)(xf取得极大值)(1xf，在2xx 处)(xf取得极小值)(2xf． 2.0a时)(xf在),(1xx或),(2  xx单调递减；)(xf在),(21 xxx 单调递增在1xx 处)(xf取得极小值)(1xf，在2xx 处)(xf取得极大值)(2xf． 2 注意：三次函数f(x)有极值导函数(x )f 的判别式0 3.一般地dcxbxaxxf23)()0(a在导数023)(2cbxaxxf有两根,,21 xx且21xx 时，在1x 处有1( )()f xf xM极大值；在2x 处有2( )()f xf xm极小值， 4 .三次方程根的个数问题，由三次函数图象极易得到以下结论: 若 yf x为三次函数,其导数为  yfx,则: ⑴若( )0fx或( )0fx恒成立,则 0f x 仅有一实数解。 ⑵若( )0fx有两个不等实数解,m n 则: ① 若   0nfmf,则 0f x 有一实数解. ② 若   0nfmf,则 0f x 有二个不等实数解. ③ 若   0nfmf,则 0f x 有三个不等实数解. (注:①、③可进一步推广) 专题二 三次函数的对称性 我们知道，二次函数)0()(2acbxaxxf是轴对称图形，其对称轴方程式是abx2。三次函数cxaxxf3)(是奇函数，其图象关于点)0,0(对称，三次函数dbxaxxf3)(的图象关 于 点),0(d对 称 ，那 么 对 于 一般的三次函数)0()(23adcxbxaxxf有没有对称中心呢？答案是肯定的，有对称中心，其对称中心是))3(,3(abfab。下面给出证明。 证明 1：二次函数通过配方可以消去一次项。类似得，三次函数通过配方可以消去二次项。 3 dcxbxaxxf23)(dcxabaxabaabxabxabxa323223)3()3(3])3()3(333[ dabaxcabaabxa...