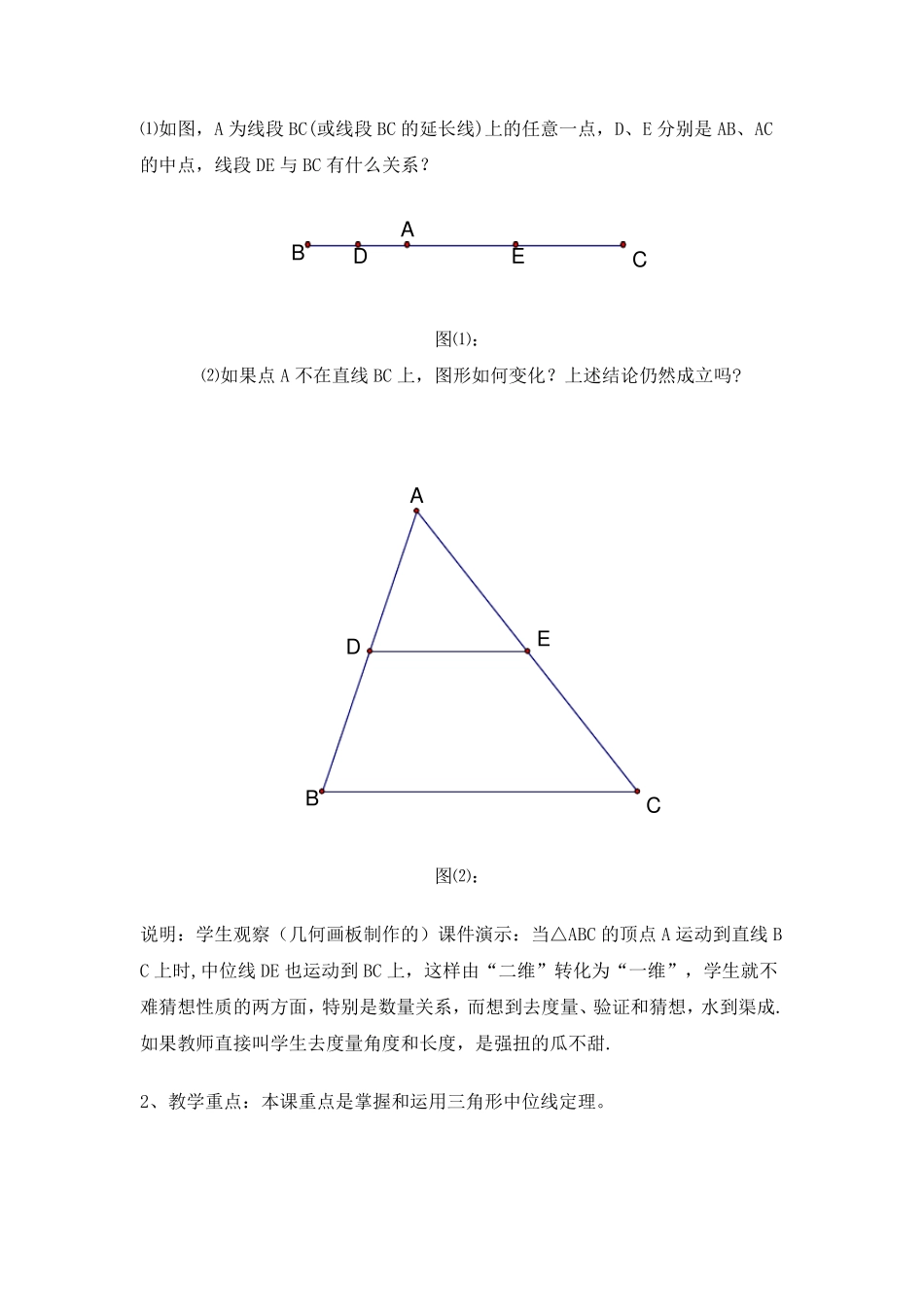
三角形中位线定理的证明及其教学说明 以 下内容作者为:青岛第四中学杨瀚书老师 一、 三角形中位线定理的几种证明方法 法 1: 如图所示,延长中位线DE 至 F,使 ,连结 CF,则 ,有 AD FC,所以 FC BD,则四边形BCFD 是平行四边形,DF BC。因为 ,所以 DE BC21. 法 2:如图所示,过C 作 交 DE 的延长线于 F,则 ,有 FC AD,那么 FC BD,则四边形BCFD 为平行四边形,DF BC。因为 ,所以 DE BC21. 法 3:如图所示,延长DE 至 F,使 ,连接 CF、DC、AF,则四边形ADCF 为平行四边形,有 AD CF,所以 FC BD,那么四边形BCFD 为平行四边形,DF BC。因为 ,所以 DE BC21. 法4:如图所示,过点E 作MN∥AB,过点A 作AM∥BC,则四边形ABNM 为平行四边形,易证CENAEM,从而点E 是MN的中点,易证四边形ADEM和BDEN都为平行四边形,所以DE=AM=NC=BN,DE∥BC,即DEBC21。 法5:如图所示,过三个顶点分别向中位线作垂线. 二、教学说明 1、三角形中位线定理的另外一种猜想过程:“二维”转化为“一维” 在引导学生探索三角形中位线定理时,由于学生画出中位线后,就不难直观地发现平行关系,难的是发现数量关系,我联想到在此之前认识线段中点时的一道典型例题,挖掘它与原有知识的内在联系,从而作如下探索引导。 ⑴如图,A 为线段BC(或线段BC 的延长线)上的任意一点,D、E 分别是AB、AC的中点,线段DE 与BC 有什么关系? 图⑴: ⑵如果点A 不在直线BC 上,图形如何变化?上述结论仍然成立吗? 图⑵: 说明:学生观察(几何画板制作的)课件演示:当△ABC 的顶点A 运动到直线BC 上时,中位线DE 也运动到BC 上,这样由“二维”转化为“一维”,学生就不难猜想性质的两方面,特别是数量关系,而想到去度量、验证和猜想,水到渠成.如果教师直接叫学生去度量角度和长度,是强扭的瓜不甜. 2、教学重点:本课重点是掌握和运用三角形中位线定理。 EDABCEDABC第一,要知道中位线定理的作用:可以证明两条直线平行及线段的倍分关系,计算边长或中位线的长。 第二,要知道中位线定理的使用形式,如: DE 是△ABC 的中位线 ∴ DE∥BC, BCDE21 第三,让学生通过部分题目进行训练,进而掌握和运用三角形中位线定理。 题1 如图4.11-7,Rt△ABC,∠BAC=90°,D、E 分别为 AB,BC 的中点,点 F 在 CA 延长线上,∠FDA=∠B. (1)求证:AF=DE;(2)若 AC=6...