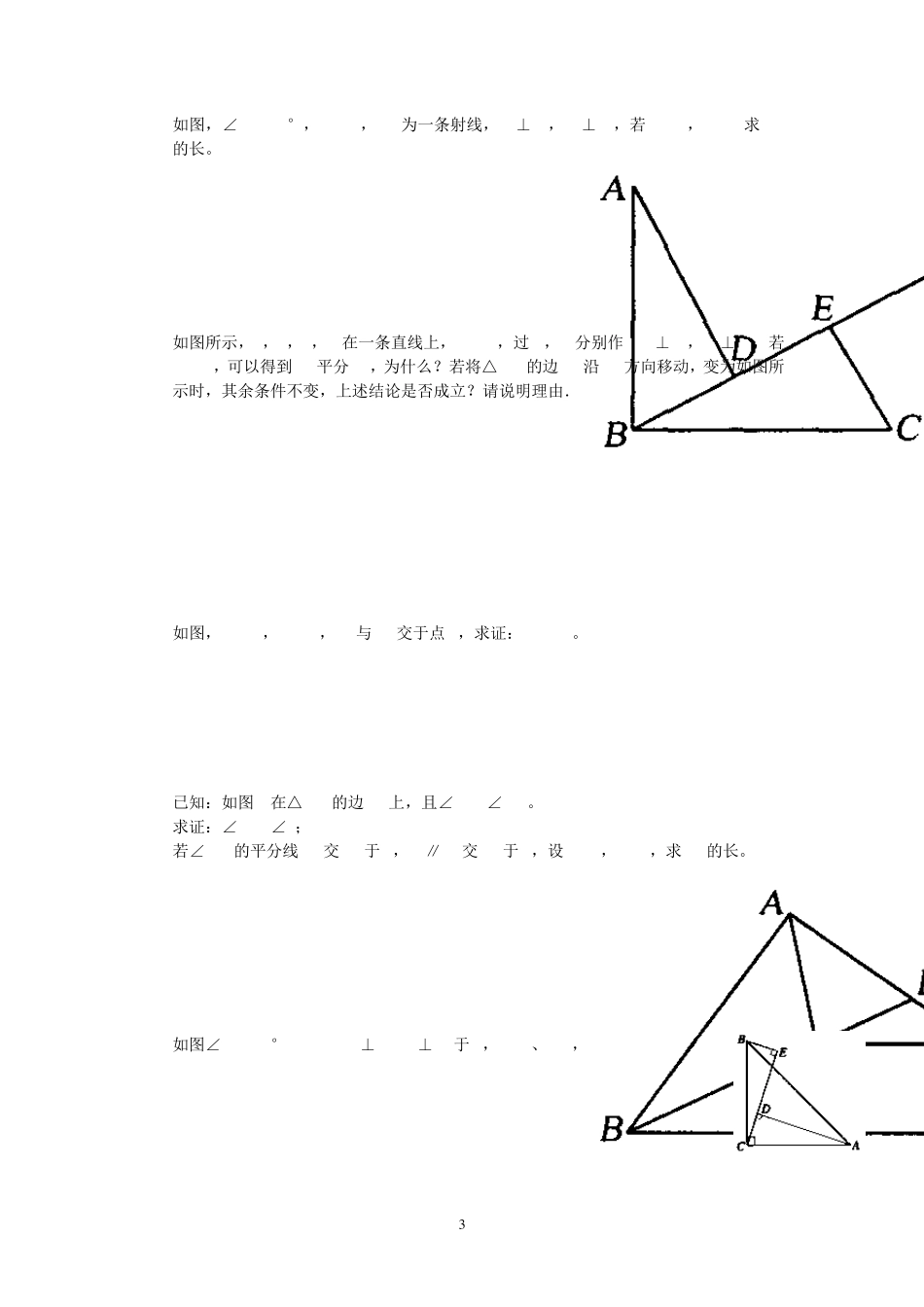
1 三角形全等证明经典试题 1. 已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF. 求证:AC∥DF. 2. 如图,已知: AD是BC上的中线 ,且DF=DE.求证:BE∥CF. 3. 如图, 已知:AB⊥BC于B , EF⊥AC于G , DF⊥BC于D , BC=DF.求证:AC=EF. 4. 如图,在Δ ABC中,AC=AB,AD是BC边上的中线,则AD⊥BC,请说明理由。 5. 如图,已知AB=DE,BC=EF,AF=DC,则∠EFD=∠BCA,请说明理由。 6. 如图,在Δ ABC中,D是边BC上一点,AD平分∠BAC,在AB上截取 AE=AC,连结 DE,已知DE=2cm,BD=3cm,求线段 BC的长。 FGEDCBAABCDEABCDEFABCD 2 FEDCBA7. 如图,Δ ABC的两条高AD、BE相交于H,且AD=BD,试说明下列结论成立的理由。 (1)∠DBH=∠DAC;(2)Δ BDH≌Δ ADC。 8. 如图,已知ABC为等边三角形,D 、E、F 分别在边BC 、CA 、AB 上,且DEF也是等边三角形. (1)除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的; (2)你所证明相等的线段,可以通过怎样的变化相互得到?写出变化过程. 9. 如图,在矩形ABCD中,F是BC边上的一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC,根据上述条件,请你在图中找出一对全等三角形,并证明你的结论。 10. 已知:如图所示,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,•PN⊥CD于N,判断PM与PN的关系. 11. 如图所示,P为∠AOB的平分线上一点,PC⊥OA于C,•∠OAP+∠OBP=180°,若 OC=4cm,求 AO+BO的值. ABCDEHPDACBMNPDACBO 3 12. 如图,∠ABC=90°,AB=BC,BP为一条射线,AD⊥BP,CE⊥PB,若 AD=4,EC=2.求 DE的长。 i. 13. 如图所示,A,E,F,C在一条直线上,AE=CF,过 E,F分别作 DE•⊥AC,BF⊥AC,若AB=CD,可以得到 BD平分 EF,为什么?若将△DEC的边 EC沿 AC方向移动,变为如图所示时,其余条件不变,上述结论是否成立?请说明理由. 14. 如图,OE=OF,OC=OD,CF与 DE交于点 A,求证: AC=AD。 15. 已知:如图E在△ABC的边 AC上,且∠AEB=∠ABC。 (1) 求证:∠ABE=∠C; (2) 若∠BAE的平分线 AF交 BE于 F,FD∥BC交 AC于 D,设 AB=5,AC=8,求 DC的长。 16. 如图∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于 D,AD=2、5cm,DE=1.7cm,求 BE长 GDFACBEGDFACBEFEDCAO 4 17. 如图,D是等边△ABC的边AB上的一动点,以CD为一边向上作等边△EDC,连接AE,找出图中的一组全等三角形...