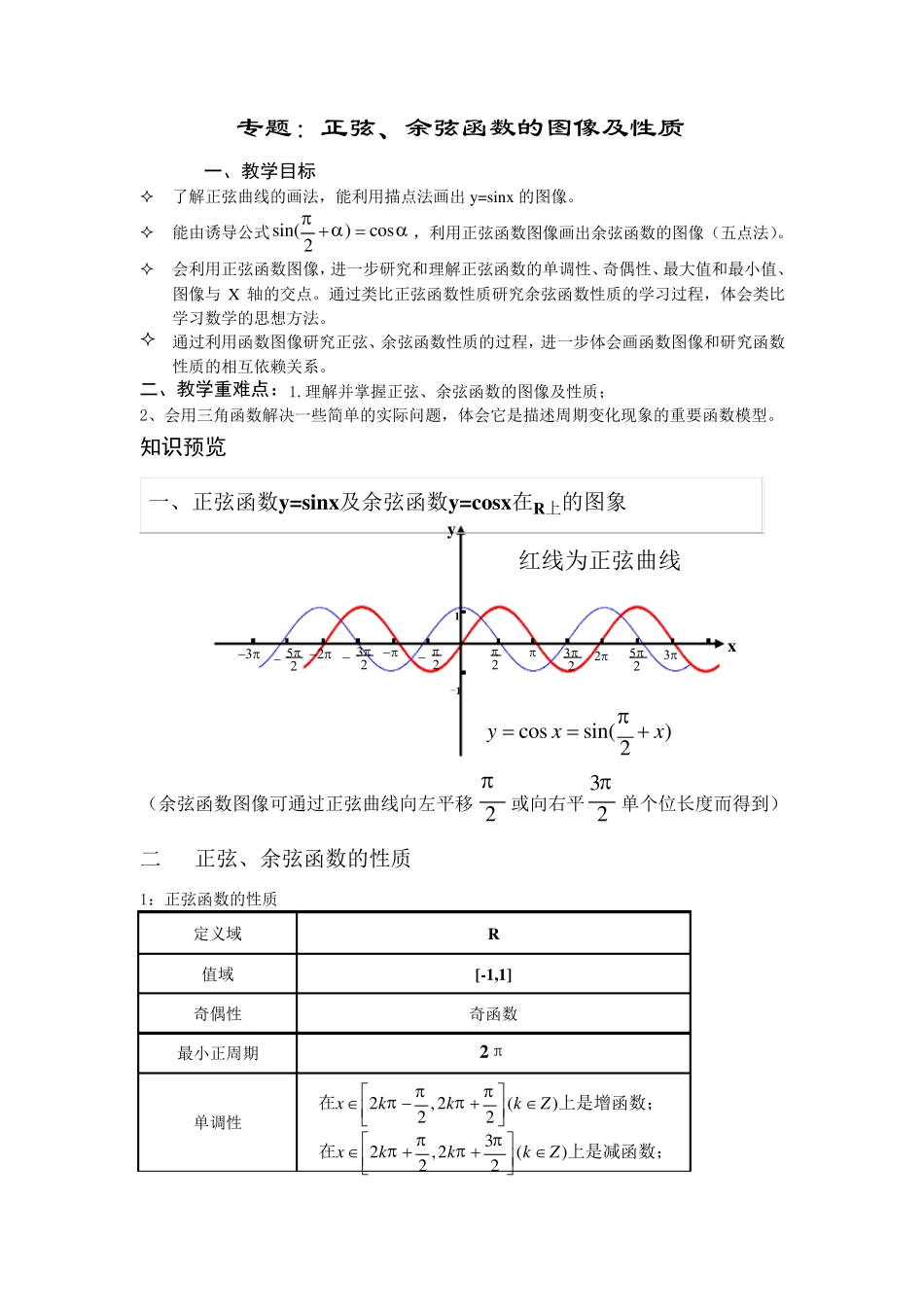
专题:正弦、余弦函数的图像及性质 一、教学目标 了解正弦曲线的画法,能利用描点法画出y=sinx 的图像。 能由诱导公式sin()cos2,利用正弦函数图像画出余弦函数的图像(五点法)。 会利用正弦函数图像,进一步研究和理解正弦函数的单调性、奇偶性、最大值和最小值、图像与X 轴的交点。通过类比正弦函数性质研究余弦函数性质的学习过程,体会类比学习数学的思想方法。 通过利用函数图像研究正弦、余弦函数性质的过程,进一步体会画函数图像和研究函数性质的相互依赖关系。 二、教学重难点:1.理解并掌握正弦、余弦函数的图像及性质; 2、会用三角函数解决一些简单的实际问题,体会它是描述周期变化现象的重要函数模型。 知识预览 (余弦函数图像可通过正弦曲线向左平移2或向右平32单个位长度而得到) 二 正弦、余弦函数的性质 1:正弦函数的性质 定义域 R 值域 [-1,1] 奇偶性 奇函数 最小正周期 2π 单调性 x y 1 -1 cossin()2yxx红线为正弦曲线 一、正弦函数y=sinx及余弦函数y=cosx在R上的图象 32,2()22xkkkZ在上是减函数;2,2()22xkkkZ在上是增函数;最值 2 余弦函数的性质 定义域 R 值域 [-1,1] 奇偶性 偶函数 最小正周期 2π 单调性 最值 对称坐标:正弦曲线是中心对称图形,对称坐标(,0)()kkZ,关于原点对称, 余弦曲线是中心对称图形,对称坐标 (,0)()2kkZ 对称轴方程:正弦曲线是轴对称图形,对称轴方程2xkkZ() 余弦曲线是轴对称图形:对称轴方程xkkZ() 需要注意的问题: 在考察基础题时,要求几个知识点的综合运用,注意各知识点之间的联系。 加大联系力度,解决公式的综合运用问题,提高计算能力。 掌握好正弦、余弦函数和sin()yAt的图像和性质(定义域、值域、最值、周期及单调性、奇偶性),它们也是新课改高考常考内容之一 掌握几种数学思想在三角函数问题中的应用:树形结合、整体思想,代换思想,化归思想 要注意知识外延和横向联系,特别是重视代数、不等式、函数、三角函数的综合运用。 三:应用举例 【例 1】请在下图分别画出正弦函数、余弦函数在[0,2π]的图象。 y y x x max2()12xkkZy当时,min32()12xkkZy ...