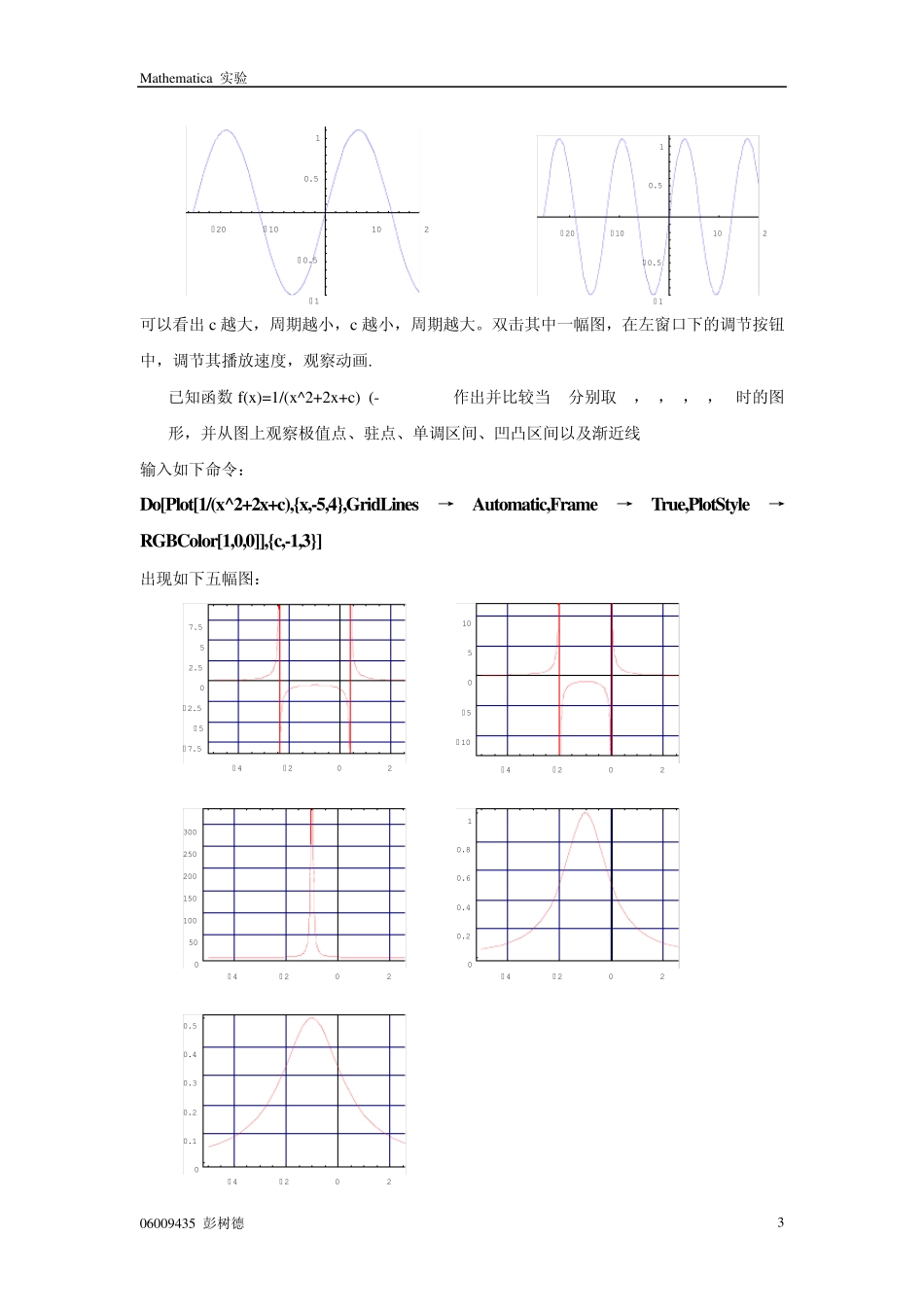
Mathematica 实验 06009435 彭树德 1 高等数学实验报告 班级:0 6 0 0 9 4 学号:0 6 0 0 9 4 3 5 姓名:彭树德 Mathematica 实验 06009435 彭树德 2 高等数学实验报告 学号:06009435 姓名:彭树德 实验目的:了解Mathematica 软件并运用。通过用Mathematica 软件更加深刻地理解、熟悉高等数学中的知识,学会用Mathematica 来处理一些数学上繁琐的问题来帮助自己更好地理解和掌握。实际 实验题: 实验二 一元函数图形及其性质 1. 制作函数y =sin cx 的图形动画,并观察参数c 对函数图形的影响. 输入如下命令: Do[Plot[Sin[c*x],{x,-2Pi,2Pi},PlotRange→All,PlotStyle→RGBColor[0,0,1]],{c,1,4}] 出现如下四幅图: -6-4-224-1-0.50.51 -6-4-224-1-0.50.51 -6-4-224-1-0.50.51 -6-4-224-1-0.50.51 输入如下命令: Do[Plot[Sin[c*x],{x,-8Pi,8Pi},PlotRange→All,PlotStyle→RGBColor[0,0,1]],{c,1/4,1/2,1/4}] 出现如下两幅图: Mathematica 实验 06009435 彭树德 3 -20-10102-1-0.50.51 -20-10102-1-0.50.51 可以看出c 越大,周期越小,c 越小,周期越大。双击其中一幅图,在左窗口下的调节按钮中,调节其播放速度,观察动画. 2. 已知函数f(x )=1/(x ^2+2x +c) (-5<=x<=4),作出并比较当c分别取-1,0,1,2,3时的图形,并从图上观察极值点、驻点、单调区间、凹凸区间以及渐近线. 输入如下命令: Do[Plot[1/(x^2+2x+c),{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]],{c,-1,3}] 出现如下五幅图: -4-202-7.5-5-2.502.557.5 -4-202-10-50510 -4-202050100150200250300 -4-20200.20.40.60.81 -4-20200.10.20.30.40.5 Mathematica 实验 06009435 彭树德 4 观察图可得: 第一幅图:极大值点为x =-1,驻点为x =-1,单调区间为增(-∞,-1-√2)、(-1-√2,-1),减(-1,-1+√2)、(-1+√2,+ ∞),凸区间为(-∞,-1-√2) 、(-1+√2,+ ∞),凹区间为(-1-√2,-1+√2),渐近线为水平y=0,垂直x=-1-√2,x=-1+√2. 第二幅图:极大值点为x=-1,驻点为x=-1,单调区间为增(-∞,-2)、(-2,-1),减(-1,0)、(0, + ∞),凸区间为(-∞,-2) 、(0, + ∞),凹区间(-2,0). 第三幅图:没有极值点,没有驻点,单调区间为增(-∞,-1),减(-1, + ∞),凸区间为(-∞,-1)、 (-1, + ∞). 第四幅图:极大值点为x=-1,驻点为x=-1,单调区间为增(-∞,-1),减(-1, +...