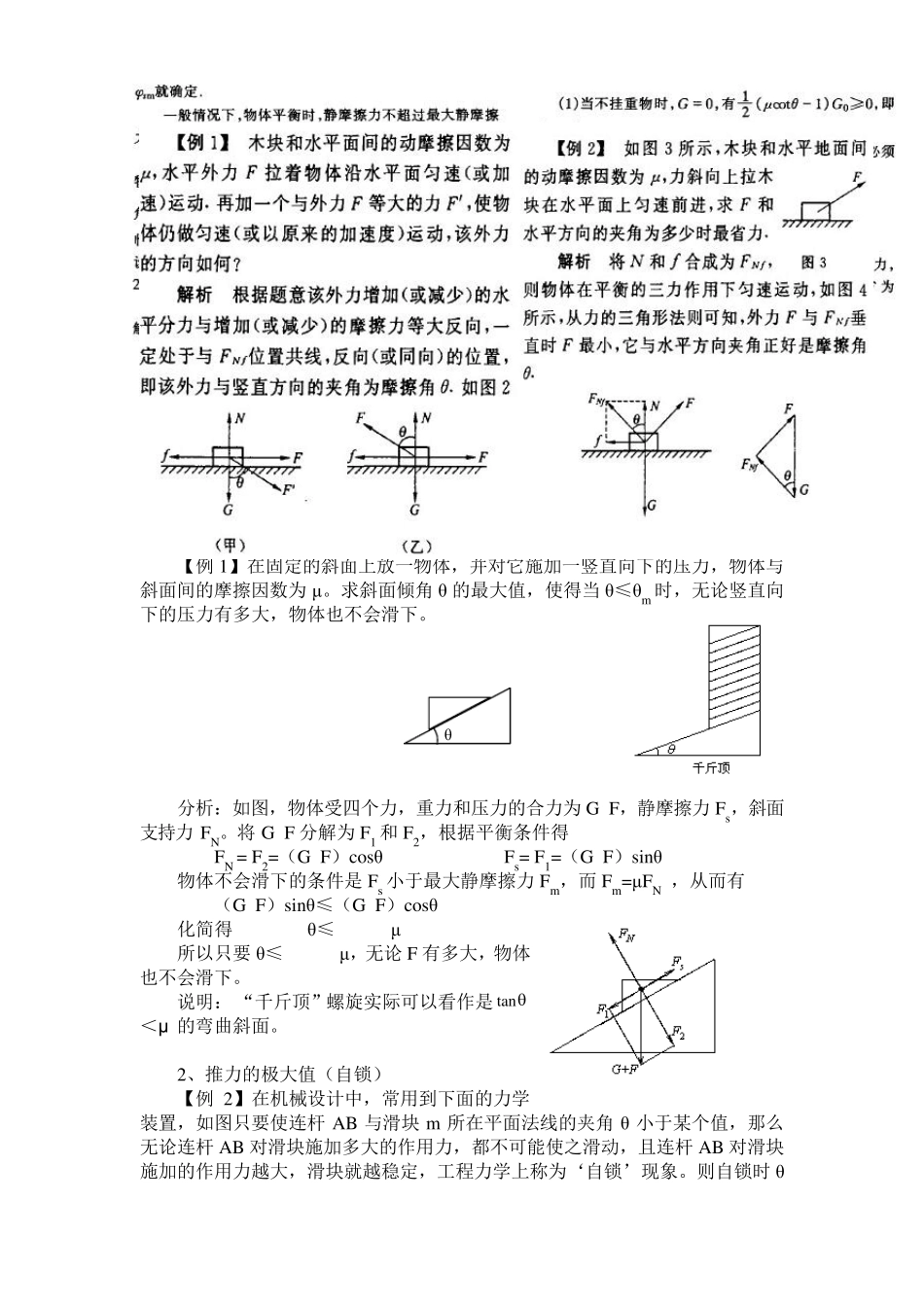
摩 擦 角概念和计算 1、“千斤顶”中的学问 【例 1】在固定的斜面上放一物体,并对它施加一竖直向下的压力,物体与斜面间的摩擦因数为 μ。求斜面倾角 θ 的最大值,使得当 θ≤θm 时,无论竖直向下的压力有多大,物体也不会滑下。 分析:如图,物体受四个力,重力和压力的合力为 G+F,静摩擦力 Fs,斜面支持力 FN。将 G+F 分解为 F1 和 F2,根据平衡条件得 FN = F2=(G+F)cosθ Fs= F1=(G+F)sinθ 物体不会滑下的条件是 Fs 小于最大静摩擦力 Fm,而 Fm=μFN ,从而有 (G+F)sinθ≤(G+F)cosθ 化简得 θ≤arctanμ 所以只要 θ≤arctanμ,无论 F 有多大,物体也不会滑下。 说明: “千斤顶”螺旋实际可以看作是tan<μ 的弯曲斜面。 2、推力的极大值(自锁) 【例 2】在机械设计中,常用到下面的力学装置,如图只要使连杆 AB 与滑块 m 所在平面法线的夹角 θ 小于某个值,那么无论连杆 AB 对滑块施加多大的作用力,都不可能使之滑动,且连杆 AB 对滑块施加的作用力越大,滑块就越稳定,工程力学上称为‘自锁’现象。则自锁时 θθ 应满足什么条件?设滑块与所在平面间的动摩擦因数为 μ。 分析:将连杆 AB 对滑块施加的推力 F 分解,且 F远远大于 mg,可以忽略。则滑块 m 不产生滑动的条件为 Fsinθ<μFcosθ 化简得自锁的条件为 θ<arctanμ。 3、运动员的弯道技术 【例 3】在田径比赛、摩托车赛、自行车赛等运动项目中,当通过弯道时,运动员必须倾斜与路面保持一定的角度 θ 才能顺利通过弯道,这就是运动员的弯道技术。路面的弯道半径越小,运动员的速度越快,运动员的倾斜角就越大。设在摩托车比赛中,摩托车与路面间的摩擦因数为 μ,试求摩托车所能达到的最大倾角。 分析:运动员要稳定地平动,路面对摩托车的力必须通过整体的重心,所以静摩擦力 F1 与支持力 F2 的夹角等于运动员与路面的倾斜角度 。而路面对摩托车整体的力 F 是 F1 和 F2 的合力,由图知 F1= F2tanθ=mg tanθ 对摩托车的最大静摩擦力为 Fm=μF2=μmg 则摩托车不倾倒的条件是 F1≤Fm 化简得 θ≤arctanμ 所以摩托车所能达到的最大倾角为 θm= arctanμ。 4、拉力的极小值 【例 4】在水平面上放有一质量为 m 的物体,物体与地面的动摩擦因数为 μ,现用力 F 拉物体,使其匀速运动,怎样施加 F 才能最小。 分析:设拉力与水平面间的夹角为...