全国卷高考数学圆锥曲线大题集大全

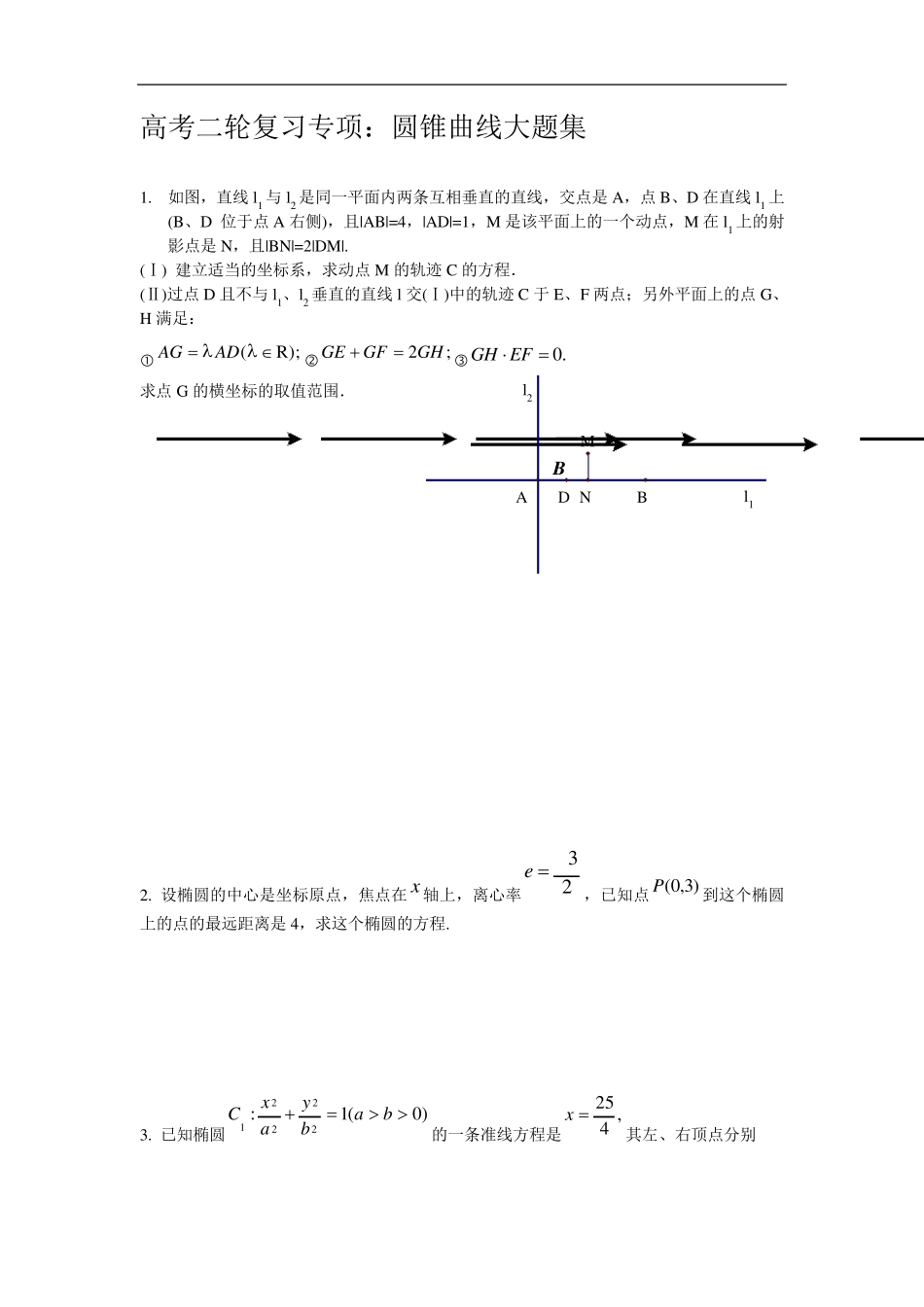
高考二轮复习专项：圆锥曲线大题集 1. 如图，直线l1 与l2 是同一平面内两条互相垂直的直线，交点是A，点B、D 在直线l1 上(B、D 位于点A 右侧)，且|AB|=4，|AD|=1，M 是该平面上的一个动点，M 在l1 上的射影点是N，且|BN|=2|DM|. (Ⅰ) 建立适当的坐标系，求动点M 的轨迹 C 的方程． (Ⅱ)过点D 且不与l1、l2 垂直的直线l 交(Ⅰ)中的轨迹 C 于E、F 两点；另外平面上的点G、H 满足： (R);AGAD2;GEGFGH0.GH EF 求点G 的横坐标的取值范围． 2. 设椭圆的中心是坐标原点，焦点在x轴上，离心率23e，已知点)3,0(P到这个椭圆上的点的最远距离是4，求这个椭圆的方程. 3. 已知椭圆)0(1:22221babyaxC的一条准线方程是,425x其左、右顶点分别 BA D M B N l2 l1 是A、B；双曲线1:22222 byaxC的一条渐近线方程为3x－5y=0. （Ⅰ）求椭圆 C1 的方程及双曲线C2 的离心率； （Ⅱ）在第一象限内取双曲线C2 上一点 P，连结 AP 交椭圆 C1 于点 M，连结 PB 并延长交椭圆 C1 于点 N，若MPAM . 求证：.0• ABMN 4. 椭圆的中心在坐标原点 O,右焦点 F（c,0）到相应准线的距离为1，倾斜角为45°的直线交椭圆于 A，B 两点.设 AB 中点为M，直线AB 与 OM 的夹角为 a. （1）用半焦距 c 表示椭圆的方程及 tan ; （2）若 2