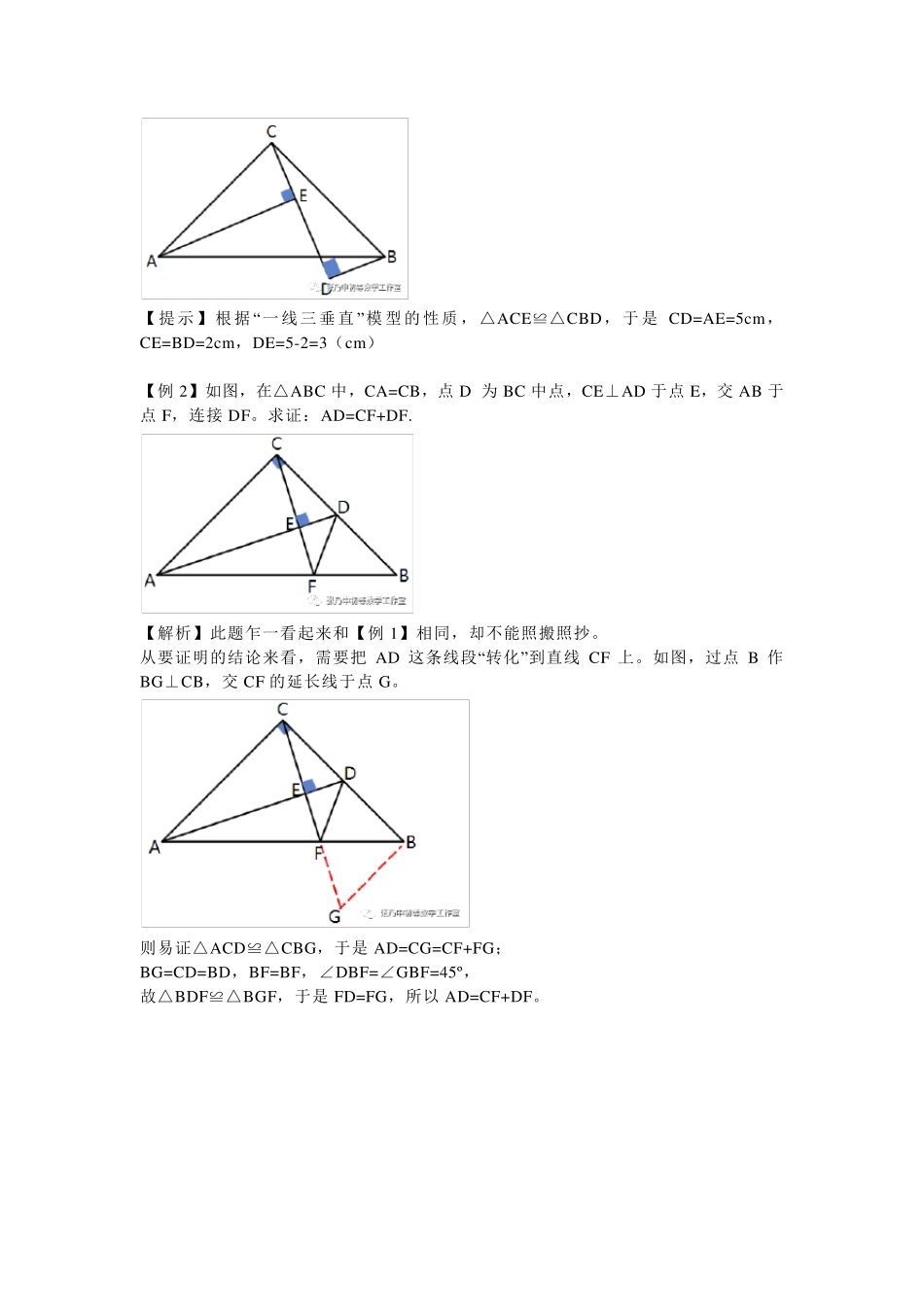
关 于 “一线三垂直”模型及其在平面几何中的应用 “一线三垂直”模型是“一线三等角”模型的特殊情况,(关于“一线三等角”模型详见比例与相似高级教程(六):相似三角形的“一线三等角”模型),即三个等角角度为90º,于是有三组边相互垂直,所以称为“一线三垂直”模型。 “一线三垂直”的性质: 1,模型中必定存在至少两个三角形相似,三对等角,三对成比例的边长; 2,当模型中有一组对应边长相等时,则模型中必定存在全等三角形。 “一线三垂直”模型在平面几何中有着及其重要的地位,常出现的图例有以下几种: 其中,在“变形2”模型下,根据相似原理,推理出了著名的“射影定理”这里主要讨论有一对对应边相等的情况。 【例1】如图,在等腰直角三角形ABC 中,∠ACB=Rt∠,AC=BC,AE⊥CE 于点 E,BD⊥CE 于点 D,AE=5cm,BD=2cm,则DE 的长为多少? 【提示】根据“一线三垂直”模型的性质,△ACE≌△CBD,于是CD=AE=5cm,CE=BD=2cm,DE=5-2=3(cm) 【例2】如图,在△ABC 中,CA=CB,点D 为BC 中点,CE⊥AD 于点E,交AB 于点F,连接DF。求证:AD=CF+DF. 【解析】此题乍一看起来和【例1】相同,却不能照搬照抄。 从要证明的结论来看,需要把AD 这条线段“转化”到直线CF 上。如图,过点B 作BG⊥CB,交CF 的延长线于点G。 则易证△ACD≌△CBG,于是AD=CG=CF+FG; BG=CD=BD,BF=BF,∠DBF=∠GBF=45º, 故△BDF≌△BGF,于是FD=FG,所以 AD=CF+DF。 关 于 “一线三垂直”模型及其在平面几何中的应用(二) “一线三垂直”的性质: 1,模型中必定存在至少两个三角形相似,三对等角,三对成比例的边长; 2,当模型中有一组对应边长相等时,则模型中必定存在全等三角形。 【例3】如图,在△ABC 中,AB=AC,∠BAC=90º,分别过 B,C 向过 A 点的直线作垂线,垂足分别为 E,F。 (1)如图1,过点 A 的直线与斜边BC 不相交时,求证:EF=EB+CF; (2)如图2,过点 A 的直线与斜边BC 相交时,其他条件不变,若 BE=10,CF=3.求EF 的长。 【提示】(1)图1 是“一线三垂直”的基础模型,△ABE≌CAF; (2)图2 是“一线三垂直”的变形4,和【例1】相同。 【例4】如图,已知△AEB 中,∠AEB=90º,以 AB 为边向外作正方形ABCD,连接AC、BD,交于点 O,连接 EO。若 BE=2,EO=3√2,求五边形AEBCD 的面积。 【解析】因为∠ABC=∠AEB=90º,故构造“一线三垂直”模型,如图。 过点C...