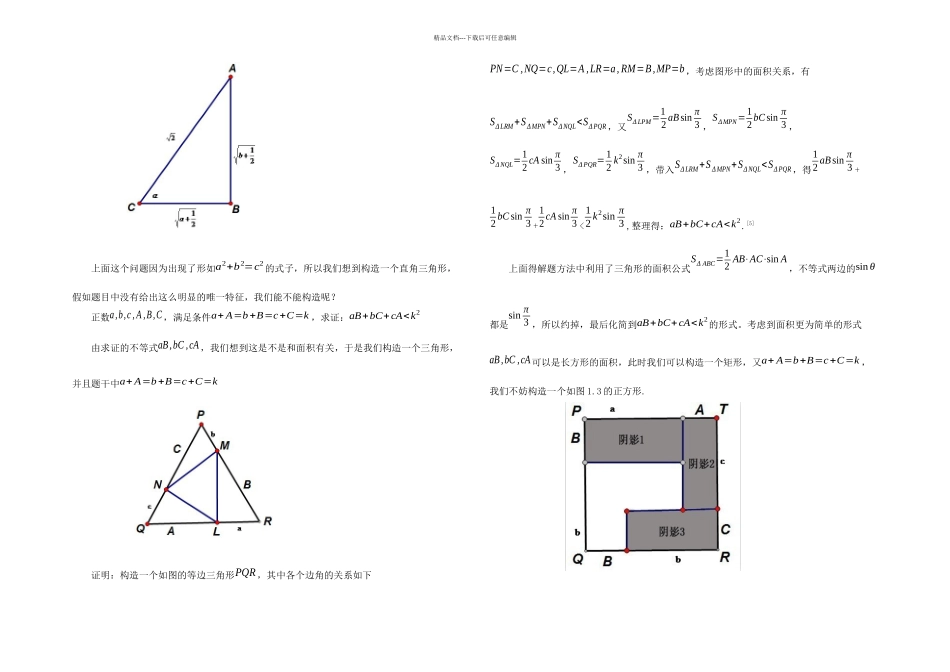
精品文档---下载后可任意编辑1.1 一个简单例子证明存在两个无理数x , y ,使z=x y 是有理数[1]传统证明方法是,假设对于任何两个无理数x , y ,都有z=x y 是无理数。那么就有(√2)√2一定是无理数,进而[(√2)√2]√2也是无理数,而[(√2)√2]√2=(√2)2=2是有理数,所以假设不成立而我们假如令x=√2, y=log2 9,我们已知和log 29都是无理数,此时x y=( √2)log29=2log23=3是有理数,问题得证。上面这个问题中我们用到的第二种方法就是中学中常用的构造法。构造法的进展历史到底什么是构造法呢?构造法就是根据固定方式,经过有限步骤能够实现的方法。引用韦尔(H.Weyl)在《数学的思维方式》一文中的一句话“当数学家们转向抽象时,有一件最为门外汉所不能理解的事情,那就是直觉的图像必须被转化为一种符号构造。”[2]这表明构造法从数学产生时就已经存在,因为数学进展所必须具备的数学符号就是用来构造对象的。除此之外,数学最初的定义有很多都是构造性的定义,比如:将线段绕其一个端点在平面内旋转一周,它的另一端点所画出的图形叫圆。构造法起源于数学之初,但它的进展是在 19 世纪末。19 世纪末,克罗内克和庞加莱基于数学的可信性,提出了“存在必须是被构造的”观点,创立了早期的直观数学学派。但是他们把直观数学推崇到极致,反对一切非构造性数学内容,搞得数学复杂难懂。随后马尔科夫提出算法数学,把一切数学概念归结为一个基本概念——算法的构造性方法。但是算法数学以递归函数为基础,大部分人同样难以理解。直到 1867 年美国数学家比肖泊发表《构造性分析》一书,摆脱了算法数学对递归函数的依赖,宣告现代构造数学的形成。时至今日,构造法不仅开创了组合数学、计算机科学等新领域,而且在数值分析,拓扑学领域也大有用武之地。[3]1.3 中学数学需要数学构造法除了高等数学,现在的中学阶段对于构造法也是相当重视的。《高中数学教学大纲》中就明确规定了学习数学不仅包括数学内容,数学语言,更重要是数学思想、方法。 在高中数学解题过程里,我们常常会遇到无从下手、常规的方法不能快速、有效解决的问题,这时我们可以另辟蹊径,利用这种特别的数学方法尝试解决问题——构造法。运用构造法解题常常是因为我们常规思维定式探求解题思路受阻,这时我们根据题设特点,用已知元素和关系式构造一个新的数学形式,如:函数、方程、图形等,这样可以绕过阻碍,得到解题的思路和方法。中学阶段应用构造法时...