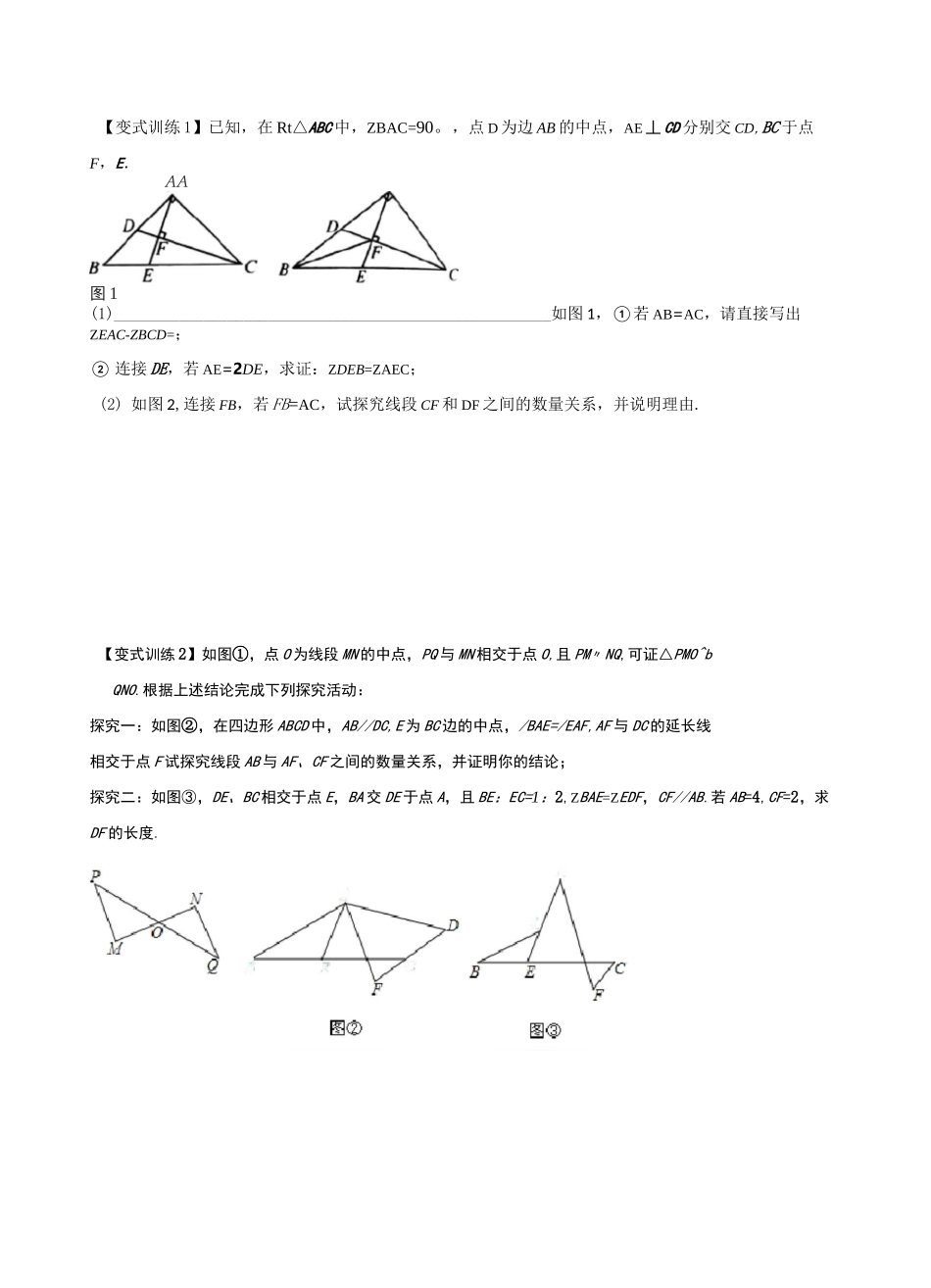
专题02 单中点与双中点模型有关中点的知识点归纳:①三角形中线平分三角形面积;②直角三角形斜边上的中线等于斜边的一半;③ 等腰三角形“三线合一”的性质;④三角形中位线平行且等于第三边的一半.在题干中,出现一个中点时,我们通常想到中线;两个中点时,想到中位线。模型一、双中点-中位线模型如图,D、E、F 分别为△ABC 三边中点,连接 DE、DF、EF,则律梟「,川丄”{',亍\打.例.如图,在 Rt^ABC 中,^ACB=90°,AC=BC,过点 C 作 CD^AB,垂足为 D,点 E 为 BC 的中点,AE 与 CD交于点 F,若 DF 的长为丰,则 AE的长为()A.<2B.2 迈 C•厉D.2*5【变式训练 1】如图,在△MC 的两边 AB、AC 向形外作正方形 ABDE 和 ACFG,取 BE、BC、CG 的中点M、Q、N.求证:MQ=QN.E【变式训练 2】如图,在平面直角坐标系中,AOAB 的顶点 B 在 x 轴正半轴上,顶点 A 和边 AB的中点 C 均【变式训练 3】如图,在 AABC 中,ZACB=60°,AC=1,D 是 AB 的中点,E 是 BC 上一点,若 DE 平分厶 ABC 的周长,则 DE 的长为模型二、单中点-倍长中线模型例.如图,CE、CB 分别是 AABC 与 AADC 的中线,且 ZACB=ZABC,AC=AB.求证:CD=2CE.DAACBE图【变式训练 1】已知,在 Rt△ABC 中,ZBAC=90。,点 D 为边 AB 的中点,AE 丄 CD 分别交 CD,BC 于点F,E.AA图 1(1)______________________________________________________如图 1,①若 AB=AC,请直接写出ZEAC-ZBCD=;② 连接 DE,若 AE=2DE,求证:ZDEB=ZAEC;(2) 如图 2,连接 FB,若 FB=AC,试探究线段 CF 和 DF 之间的数量关系,并说明理由.【变式训练 2】如图①,点 O 为线段 MN 的中点,PQ 与 MN 相交于点 O,且 PM〃NQ,可证△PMO^bQNO.根据上述结论完成下列探究活动:探究一:如图②,在四边形 ABCD 中,AB//DC,E 为 BC 边的中点,/BAE=/EAF,AF 与 DC 的延长线相交于点 F 试探究线段 AB 与 AF、CF 之间的数量关系,并证明你的结论;探究二:如图③,DE、BC 相交于点 E,BA 交 DE 于点 A,且 BE:EC=1:2,ZBAE=ZEDF,CF//AB.若 AB=4,CF=2,求DF 的长度.【变式训练 3】如图,过边长为 3 的等边△血 C 的边 AB 上一点 P,作 PE 丄 AC 于 E,Q 为 BC 延长线上一点,当 PA=CQ 时,连 PQ 交 AC 边于 D,则 DE 的长为.模型二、单中点-“三线合一”模型如图,在 AABC 中,AB=AC,D...