几何证明角平分线模型(中级)

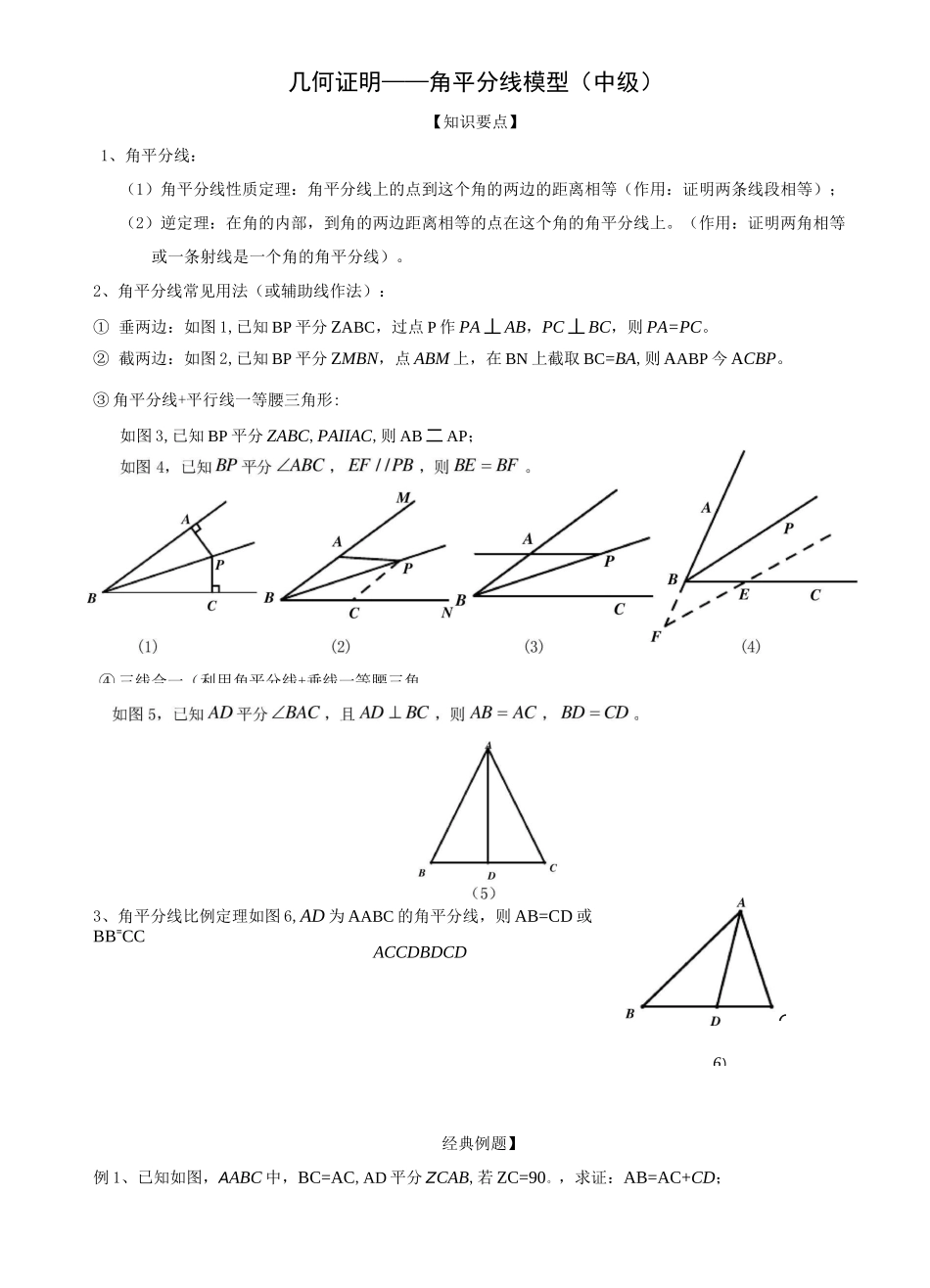
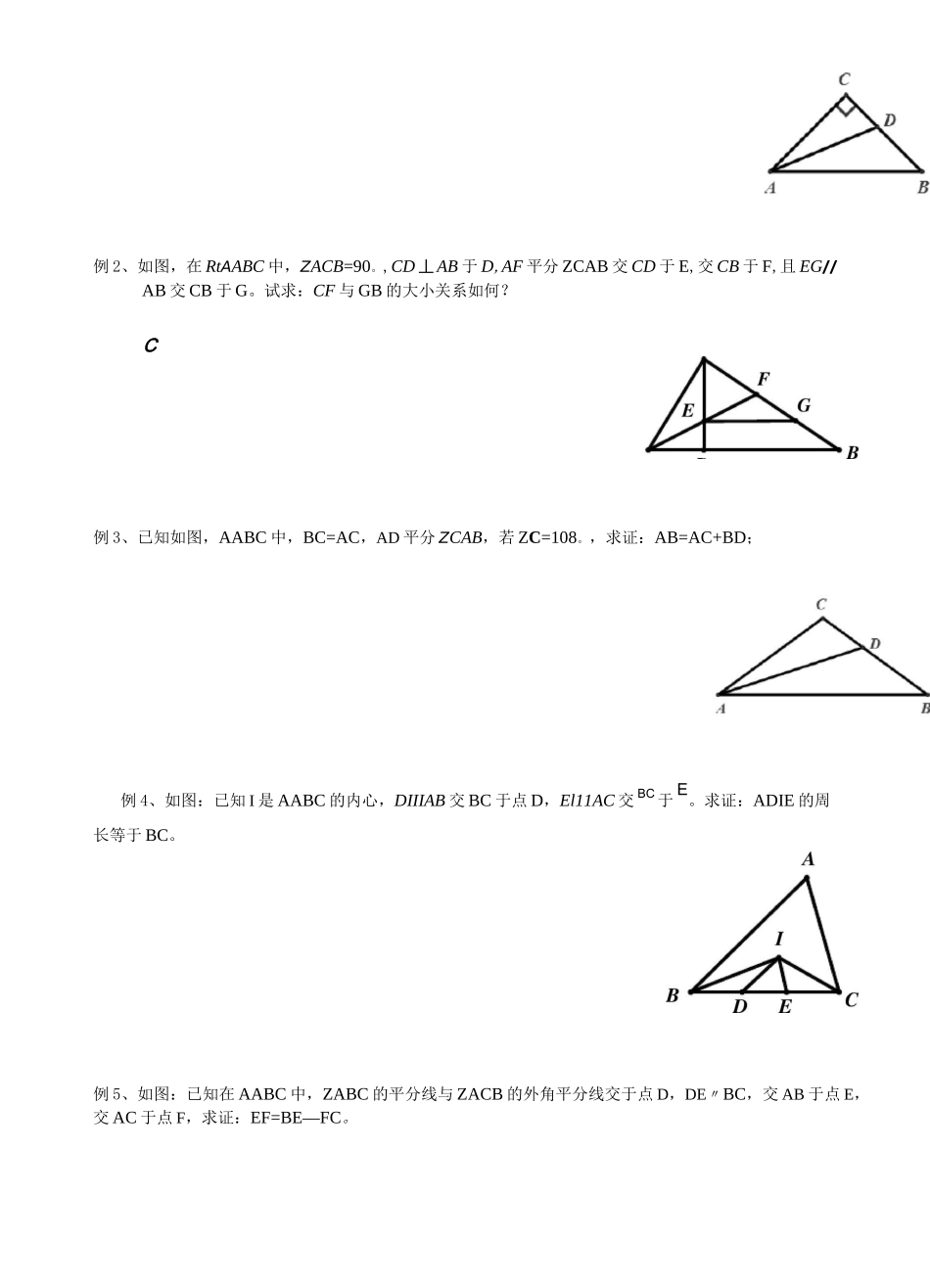
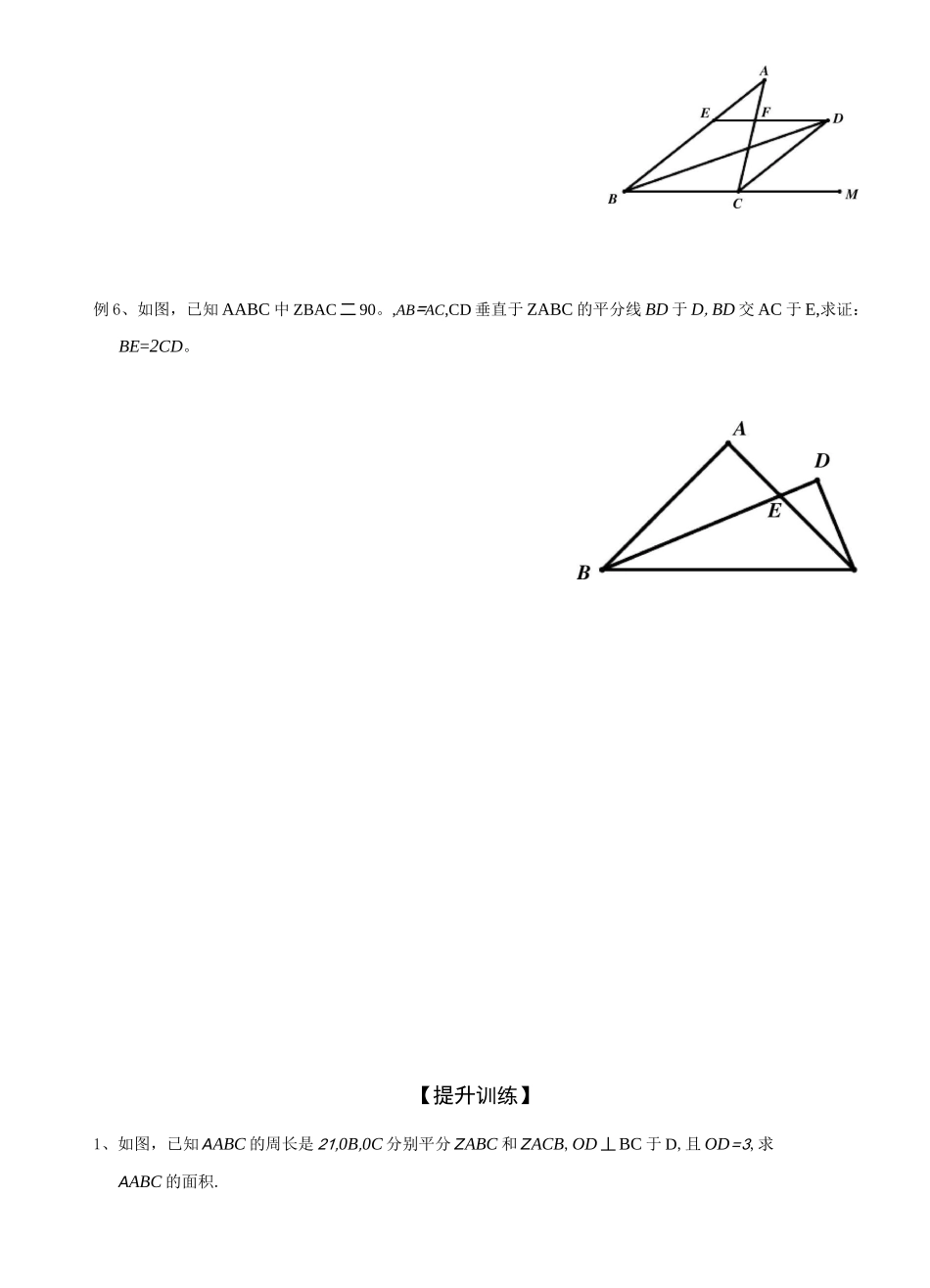
几何证明——角平分线模型（中级）【知识要点】1、角平分线：（1）角平分线性质定理：角平分线上的点到这个角的两边的距离相等（作用：证明两条线段相等）；（2）逆定理：在角的内部，到角的两边距离相等的点在这个角的角平分线上。（作用：证明两角相等或一条射线是一个角的角平分线）。2、角平分线常见用法（或辅助线作法）：① 垂两边：如图 1,已知 BP 平分 ZABC，过点 P 作 PA 丄 AB，PC 丄 BC，则 PA=PC。② 截两边：如图 2,已知 BP 平分 ZMBN，点 ABM 上，在 BN 上截取 BC=BA,则 AABP 今 ACBP。③ 角平分线+平行线一等腰三角形:如图 3,已知 BP 平分 ZABC,PAIIAC,则 AB 二 AP；3、角平分线比例定理如图 6,AD 为 AABC 的角平分线，则 AB=CD 或BB=CCACCDBDCD经典例题】例 1、已知如图，AABC 中，BC=AC,AD 平分 ZCAB,若 ZC=90。，求证：AB=AC+CD；④ 三线合一（利用角平分线+垂线一等腰三角C6）例 2、如图，在 RtAABC 中，ZACB=90。,CD 丄 AB 于 D,AF 平分 ZCAB 交 CD 于 E,交 CB 于 F,且 EG//AB 交 CB 于 G。试求：CF 与 GB 的大小关系如何？C例 3、已知如图，AABC 中，BC=AC，AD 平分 ZCAB，若 ZC=108。，求证：AB=AC+BD；例 4、如图：已知 I 是 AABC 的内心，DIIIAB 交 BC 于点 D，El11AC 交 BC于 E。求证：ADIE 的周长等于 BC。例 5、如图：已知在 AABC 中，ZABC 的平分线与 ZACB 的外角平分线交于点 D，DE〃BC，交 AB 于点 E，交 AC 于点 F，求证：EF=BE—FC。例 6、如图，已知 AABC 中 ZBAC 二 90。,AB=AC,CD 垂直于 ZABC 的平分线 BD 于 D,BD 交 AC 于 E,求证：BE=2CD。【提升训练】1、如图，已知 AABC 的周长是 21,0B,0C 分别平分 ZABC 和 ZACB,OD 丄 BC 于 D,且 OD=3,求AABC 的面积.6•已知：如图，平行四边形 ABCD 各角的平分线分别相交于点 E,F,G,H,求证：四边形 EFGH 是矩形.4.如图，AD 是厶 ABC 的角平分线，DF 丄 AB，垂足为 F,DE=DG,△ADG 和厶 AED 的面积分别为 50 和 39,求△EDF的面积.5•已知如8C7.如图，等边△ABC 中，AO 是 ZBAC 的角平分线，D 为 AO 上一点，以 CD 为一边且在 CD 下方作等边△CDE,连接 BE．(1)求证：△ACD^ABCE；(2)延长 BE 至 Q，P 为 BQ 上一点，连接 CP、CQ 使 CP=CQ=5，若 BC=8 时，求 PQ 的长.8.如图，已知在△ABC...