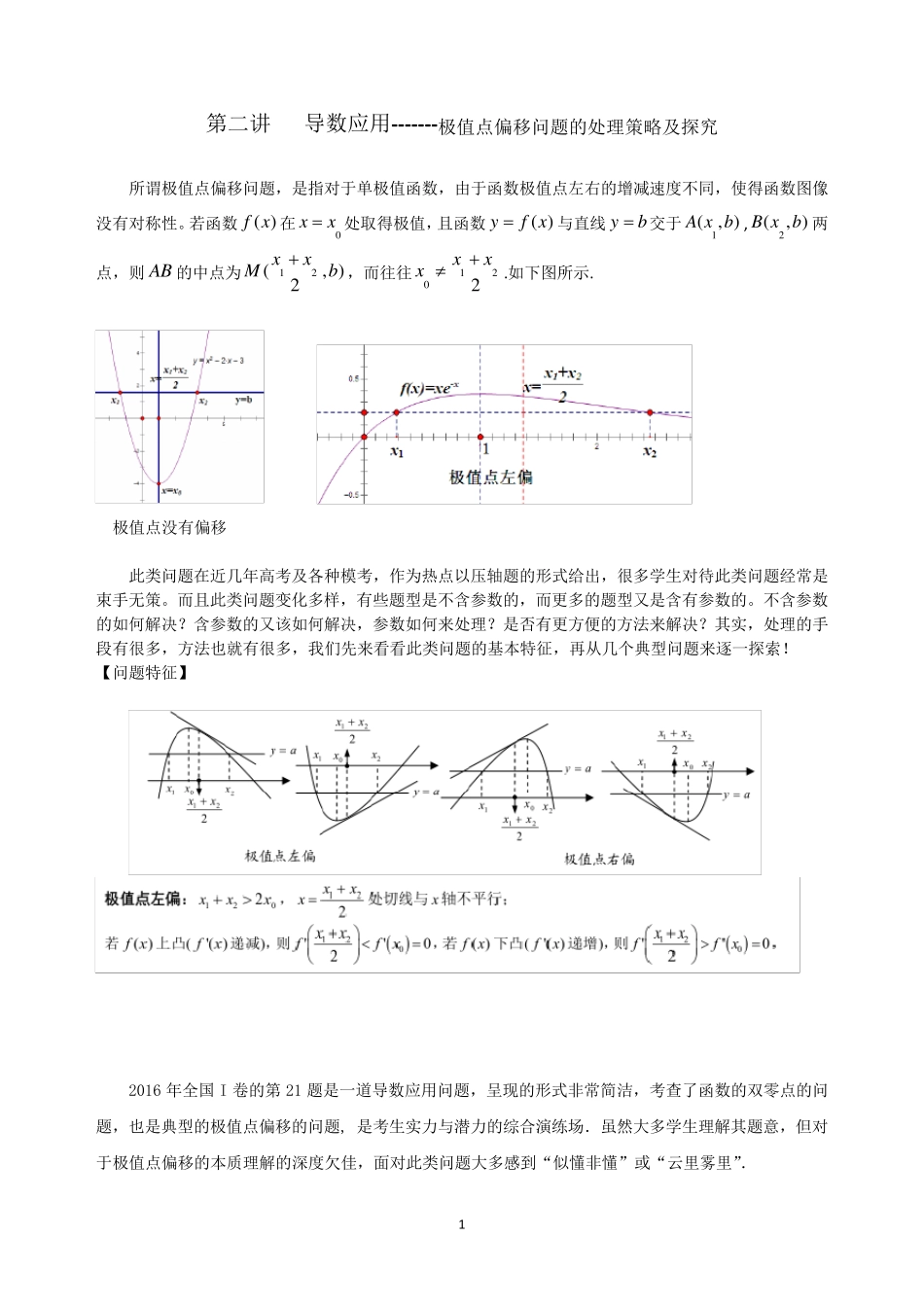
1 第 二 讲 导 数 应 用 -------极 值 点 偏 移 问 题 的 处 理 策 略 及 探 究 所 谓 极 值 点 偏 移 问 题 , 是 指 对 于 单 极 值 函 数 , 由 于 函 数 极 值 点 左 右 的 增 减 速 度 不 同 , 使 得 函 数 图 像没 有 对 称 性 。 若 函 数( )f x 在0xx处 取 得 极 值 , 且 函 数( )yf x与 直 线 yb交 于1( , )A x b ,2(, )B xb 两点 , 则 AB 的 中 点 为12(, )2xxMb, 而 往 往1202xxx.如 下 图 所 示 . 极 值 点 没 有 偏 移 此 类 问 题 在 近 几 年 高 考 及 各 种 模 考 , 作 为 热 点 以 压 轴 题 的 形 式 给 出 , 很 多 学 生 对 待 此 类 问 题 经 常 是束 手 无 策 。 而 且 此 类 问 题 变 化 多 样 , 有 些 题 型 是 不 含 参 数 的 , 而 更 多 的 题 型 又 是 含 有 参 数 的 。 不 含 参 数的 如 何 解 决 ? 含 参 数 的 又 该 如 何 解 决 , 参 数 如 何 来 处 理 ? 是 否 有 更 方 便 的 方 法 来 解 决 ? 其 实 , 处 理 的 手段 有 很 多 , 方 法 也 就 有 很 多 , 我 们 先 来 看 看 此 类 问 题 的 基 本 特 征 , 再 从几 个典型 问 题 来 逐一探 索! 【问 题 特 征 】 2016 年 全国I 卷的 第 21 题 是 一道导 数 应 用 问 题 , 呈现的 形 式 非常 简洁, 考 查了函 数 的 双零点 的 问题 , 也 是 典型 的 极 值 点 偏 移 的 问 题 , 是 考 生 实 力与 潜力的 综合演练场.虽然大多 学 生 理 解 其 题 意, 但对于 极 值 点 偏 移 的 本 质理 解 的 深度 欠佳, 面对 此 类 问 题 大多 感到“似懂非懂”或“云里雾里”. 2 一、试题再现及解析 (一)题目 (2 0 1 6 年全国 I 卷)已知函数 221xf xxea x有两个零点. (1 )求a 的取值范围; (2 )设12,x x 是 f x 的两个零点,证明:122xx. 本题第(1)小题含有参数的函数 fx 有两个零点,自然想到研究其单调性,结合零点存在性定理求得a 的取值范围是0 , .第(...