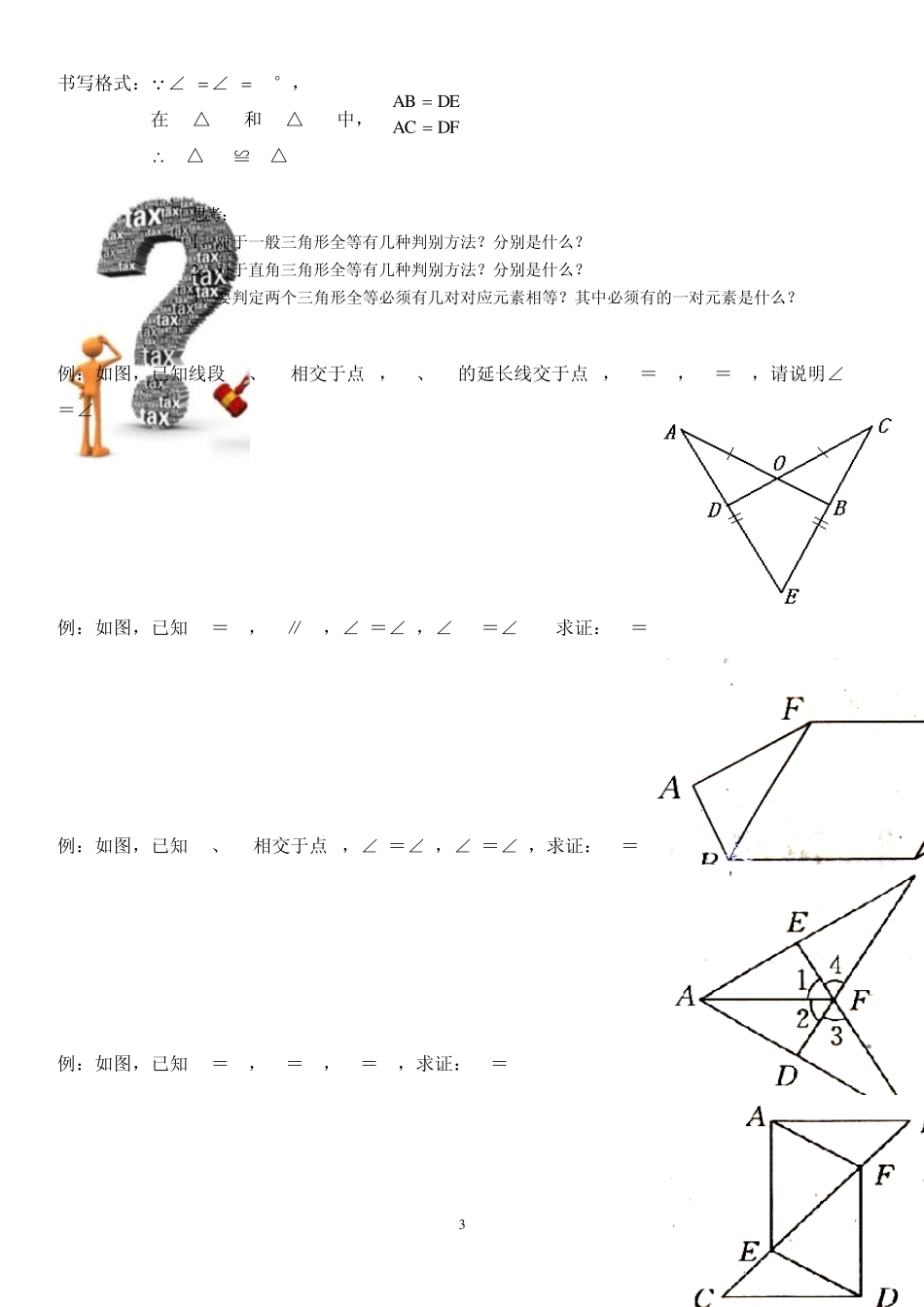
学之导教育中心教案 学生: 夏子轩 授课时间: 10月6日 课时: 2 年级: 八年级 教师: 陆老师 课 题 全等三角形的判定、角的平分线的性质 教案构架 : 一、 知识回顾 二、 知识检验 三、 知识新授 四、 知识小结 教案内容: 一、知识回顾 1、全等形的概念 2、全等三角形的定义和表示方法 3、全等三角形的性质 二、知识检验 1、如图,△ABE≌△ACD,∠D=∠E,试说明∠DAM与∠EAN的关系。 本次内容 掌握情况 总结 教 务 老 师 签 字 学 生 签 字 2 N G H M F E 2、如图,已知△EFG≌△NMH,∠F与∠M是对应角。 (1)写出相等的线段与角。 (2)若 EF=2.1cm,FH=1.1cm,HM=3.3cm,求 MN和 HG的长度。 三、知识新授 1、三角形全等的判定 三角形全等的判别方法和书写格式 SSS:三边对应相等的两个三角形全等。 SAS:两边和它们的夹角对应相等的两个三角形全等。 书写格式:在△ABC和△DEF中, 书写格式:在△ABC和△DEF中, DEAB DEAB DFAC ∠B∠E EFBC EFBC △ABC≌△DEF(SSS). △ABC≌△DEF(SAS). ASA:两角和它们的夹边对应相等 AAS:两个角和其中一个角的对应边相等 的两个三角形全等。 的两个三角形全等。 书写格式:在△ABC和△DEF中, 书写格式:在△ABC和△DEF中, ∠B∠E ∠B∠E EFBC ∠C∠F ∠C∠F DEAB △ABC≌△DEF(ASA). △ABC≌△DEF(AAS). HL:斜边和一条直角边对应相等的两个直角三角形全等。 A B C D E F A B C D E F 3 书写格式:∠B∠E90°, 在 Rt△ABC和 Rt△DEF中, Rt△ABC≌Rt△DEF(HL). 例:如图,已知线段 AB、CD相交于点 O,AD、CB的延长线交于点 E,OA=OC,EA=EC,请说明∠A=∠C. 例:如图,已知 BC=EF,BC∥EF,∠A=∠D,∠ABF=∠DEC.求证:AF=DC. 例:如图,已知 BE、CD相交于点 F,∠B=∠C,∠1=∠2,求证:DF=EF. 例:如图,已知 AB=DC,AE=DF,CE=BF,求证:AF=DE. DEAB DFAC 思考: 1、对于一般三角形全等有几种判别方法?分别是什么? 2、对于直角三角形全等有几种判别方法?分别是什么? 3、要判定两个三角形全等必须有几对对应元素相等?其中必须有的一对元素是什么? 4 例:如图,给出五个等量关系:①ADBC ,②ACBD, ③CEDE,④DC ,⑤DABCBA .请你以其中两...