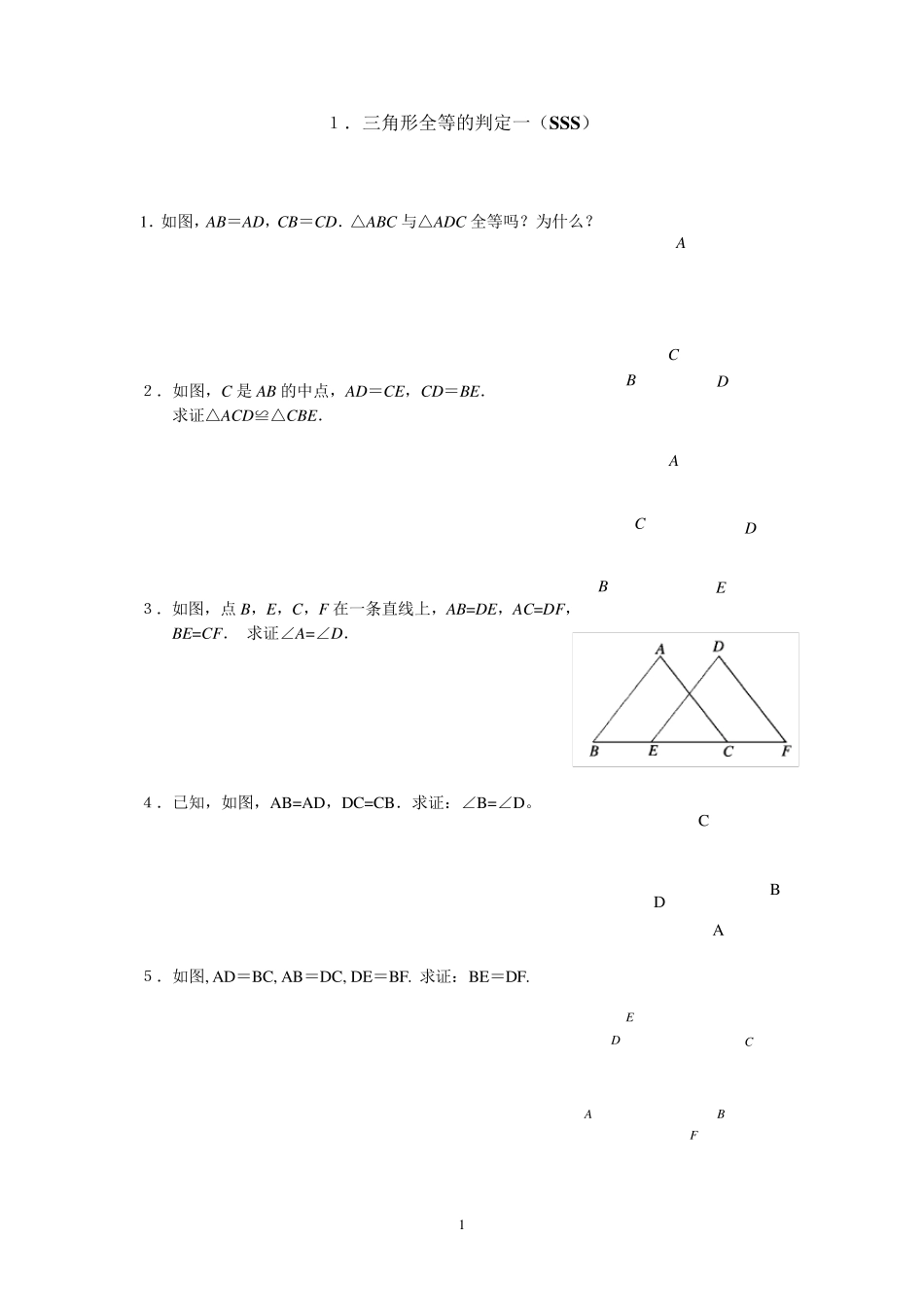
1 FEDCBA1.三角形全等的判定一(S S S ) 1.如图,AB=AD,CB=CD.△ABC 与△ADC 全等吗?为什么? 2.如图,C 是AB 的中点,AD=CE,CD=BE. 求证△ACD≌△CBE. 3.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF, BE=CF. 求证∠A=∠D. 4.已知,如图,AB=AD,DC=CB.求证:∠B=∠D。 5.如图, AD=BC, AB=DC, DE=BF. 求证:BE=DF. CDABDACBEA D C B 2 2.三角形全等的判定二(SAS) 1.如图,AC 和BD 相交于点O,OA=OC,OB=OD.求证DC∥AB. 2.如图,△ABC≌△A B C ,AD,A D 分别是△ABC,△A B C 的对应边上的中线,AD与A D 有什么关系?证明你的结论. 3.如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE 与DE 的大小与位置关系,并证明你的结论. 4.已知:如图,AD∥BC,AD=CB,求证:△ADC≌△CBA. 5.已知:如图AD∥BC,AD=CB,AE=CF。求证:△AFD≌△CEB. 6.已知,如图,AB=AC,AD=AE,∠1=∠2。求证:△ABD≌△ACE. A C E D B A E B C F D A B C D 2 A C BE D 1 3 HFEDCBA 7.已知:如图,点B,E,C,F 在同一直线上,AB∥DE,且 AB=DE,BE=CF. 求证:AC∥DF. 8.已知:如图,AD 是 BC 上的中线 ,且 DF=DE.求证:BE∥CF. 9.如图, 在△ABC 中, 分别延长中线BE、CD 至 F、H , 使 EF=BE, DH =CD, 连结 AF、AH . 求证:(1) AF=AH ; (2)点A、F、H 三点在同一直线上; (3)H F∥BC. 10.如图, 在△ABC 中, AC⊥BC, AC=BC, 直线EF 交 AC 于 F, 交 AB 于 E, 交 BC 的延长线于 D, 连结 AD、BF, CF=CD. 求证:BF=AD, BF⊥AD. 11.证明:如果两个三角形有两条边和其中一边上的中线对应相等,那么这两个三角形全等.(提示:首先分清已知和求证,然后画出图形,再结合图形用数学符号表示已知和求证) ABCDEF 4 12.证明:如果两个三角形有两条边和第三边上的中线对应相等,那么这两个三角形全等. 13.已知:如图,正方形ABCD,BE=CF,求证:(1)AE=BF; (2)AE⊥BF. 14.已知:E 是正方形ABCD 的边长AD 上一点,BF 平分∠EBC, 交 CD 于 F,求证BE=AE+CF.(提示:旋转构造等腰) 15.如图,△ABD 和△ACE 是△ABC 外两个等腰直角三角形,∠BAD=∠CAE=900.(1)判断 CD 与BE 有怎样的数量关系;(2)探索 DC 与 BE 的夹角的大小....