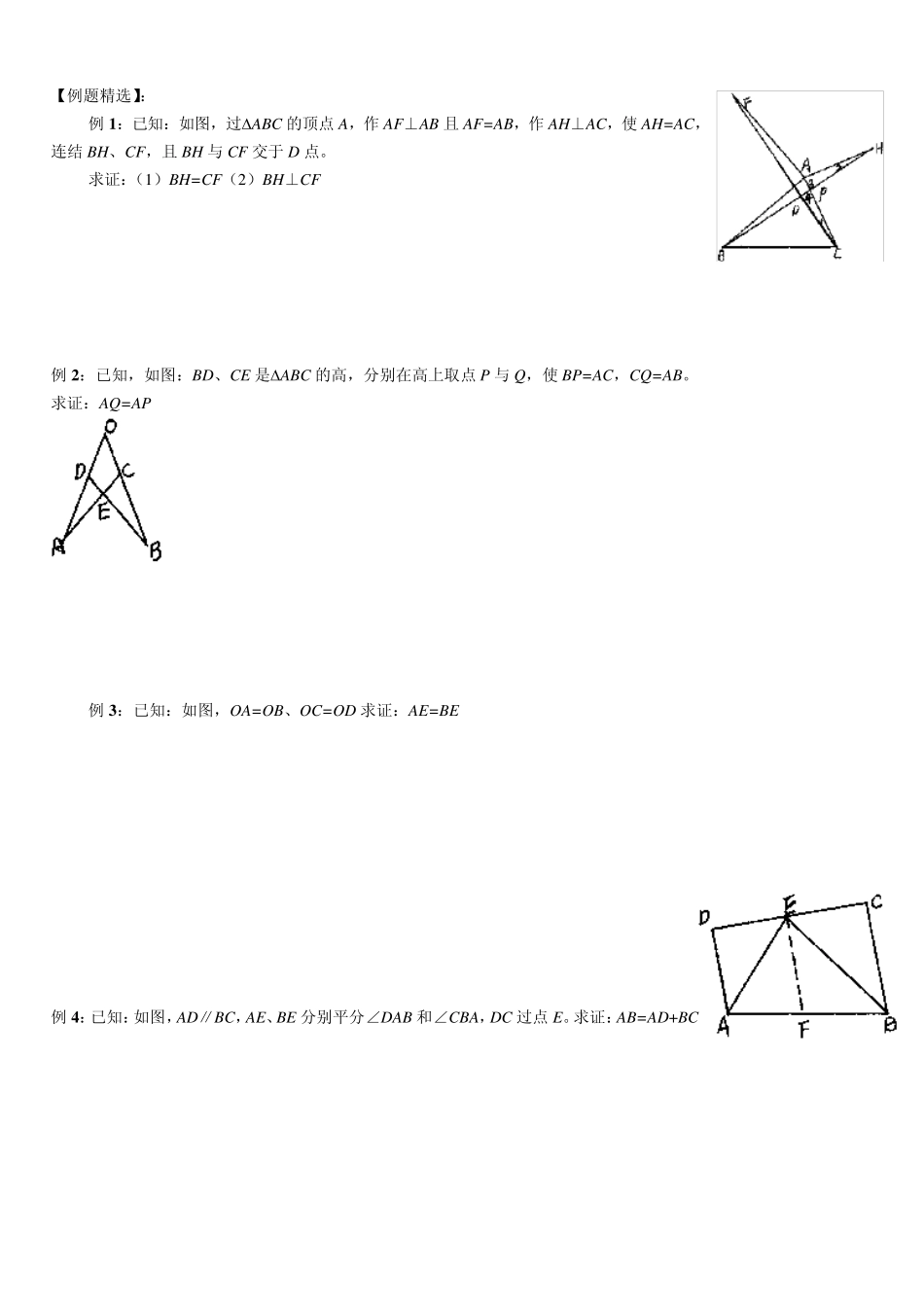
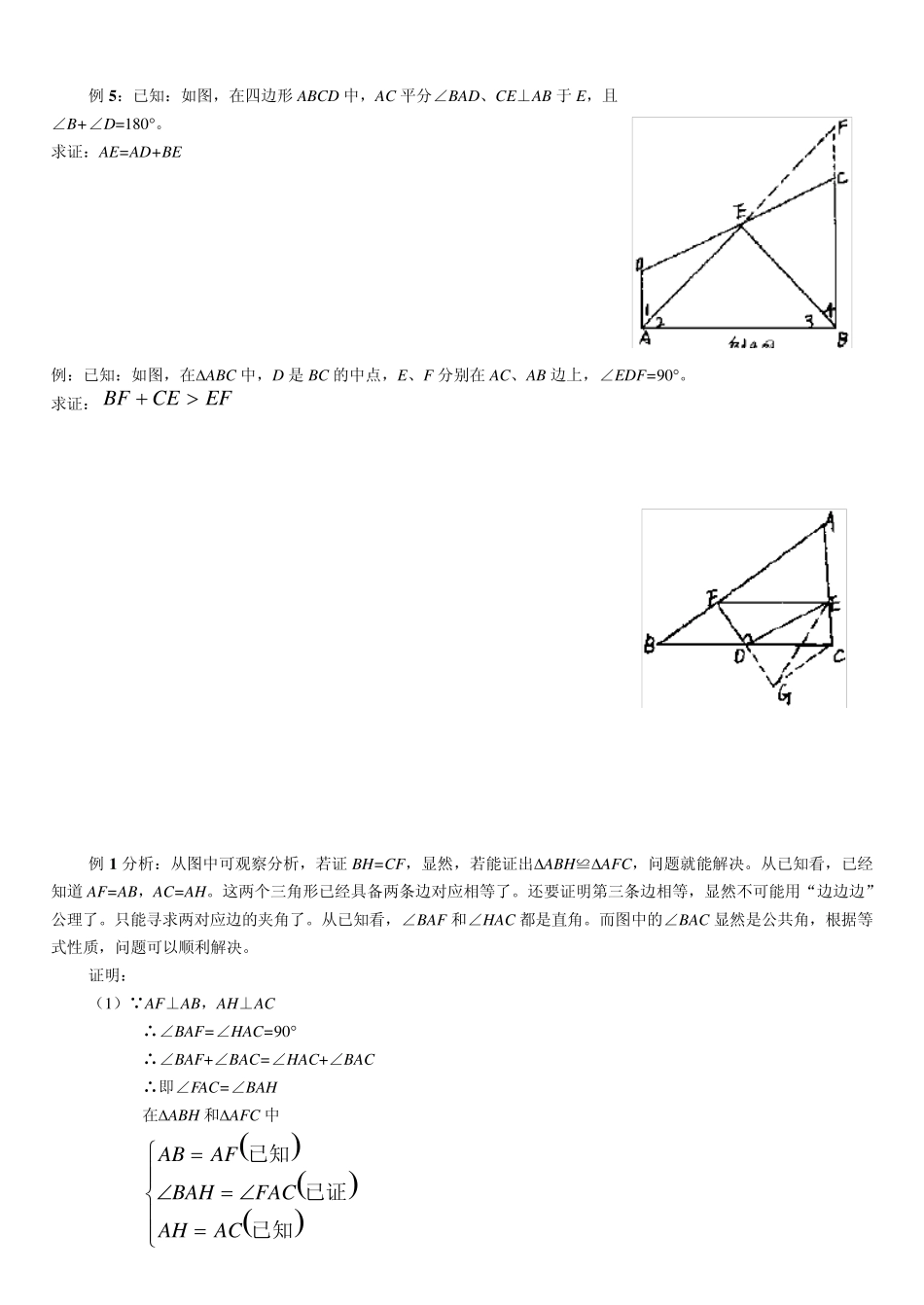
【例题精选】: 例1 :已知:如图,过ABC 的顶点A,作AF⊥AB 且AF=AB,作AH⊥AC,使AH=AC,连结BH、CF,且BH 与CF 交于D 点。 求证:(1)BH=CF(2)BH⊥CF 例2 :已知,如图:BD、CE 是ABC 的高,分别在高上取点P 与Q,使BP=AC,CQ=AB。 求证:AQ=AP 例3 :已知:如图,OA=OB、OC=OD 求证:AE=BE 例4 :已知:如图,AD∥BC,AE、BE 分别平分∠DAB 和∠CBA,DC 过点E。求证:AB=AD+BC 例5:已知:如图,在四边形ABCD 中,AC 平分∠BAD、CE⊥AB 于E,且∠B+∠D=180。 求证:AE=AD+BE 例:已知:如图,在ABC 中,D 是BC 的中点,E、F 分别在AC、AB 边上,∠EDF=90。 求证:BFCEEF 例1 分析:从图中可观察分析,若证BH=CF,显然,若能证出ABH≌AFC,问题就能解决。从已知看,已经知道AF=AB,AC=AH。这两个三角形已经具备两条边对应相等了。还要证明第三条边相等,显然不可能用“边边边”公理了。只能寻求两对应边的夹角了。从已知看,∠BAF 和∠HAC 都是直角。而图中的∠BAC 显然是公共角,根据等式性质,问题可以顺利解决。 证明: (1) AF⊥AB,AH⊥AC ∴∠BAF=∠HAC=90 ∴∠BAF+∠BAC=∠HAC+∠BAC ∴即∠FAC=∠BAH 在ABH 和AFC 中 ABAFBAHFACAHAC 已知已证已知 ∴ABH≌AFC(边角边) ∴BH=FC(全等三角形对应边相等) (2)设AC 与BH 交于点P 在APH 中 ∠HAP=90 ∴∠2+∠3=90(直角三角形中两个锐角互余) ∠1=∠2(全等三角形对应角相等) ∠3=∠4 ∴∠1+∠4=∠2+∠3=90 在PDC 中 ∠1+∠4=90 ∴∠HDC=90 ∴BH⊥CF 例 2 分析:从要证的结论 AQ=AP,只有在ABP 和QCA 中找对应原素,不难发现,已经有 BP=AC、CQ=AB,也就是这两个三角形中已经有两条对应边相等。也只有找到其中夹角相等,全等就可以了,问题的关键在于如何找出∠1=∠2?再分析已知条件,不难看出,既然 BD、CE 都是高,就有∠BDA=∠CEA=90,这样就可看出∠1 和∠2 都是∠BAC 的余角了。根据同角的余角相等这条性质得到∠1=∠2,这样问题就可以迎刃而解了。 证明: BD⊥AC 于D CE⊥AB 于E ∴∠BDA=∠CEA=90 ∴∠1+∠BAC=∠2+∠BAC=90 ∴∠1=∠2 在ABP 和PCA 中 ABCQBPAC 已知已证已知12 ∴ABP≌QCA(边角边) ∴AQ=AP(全等三角形...