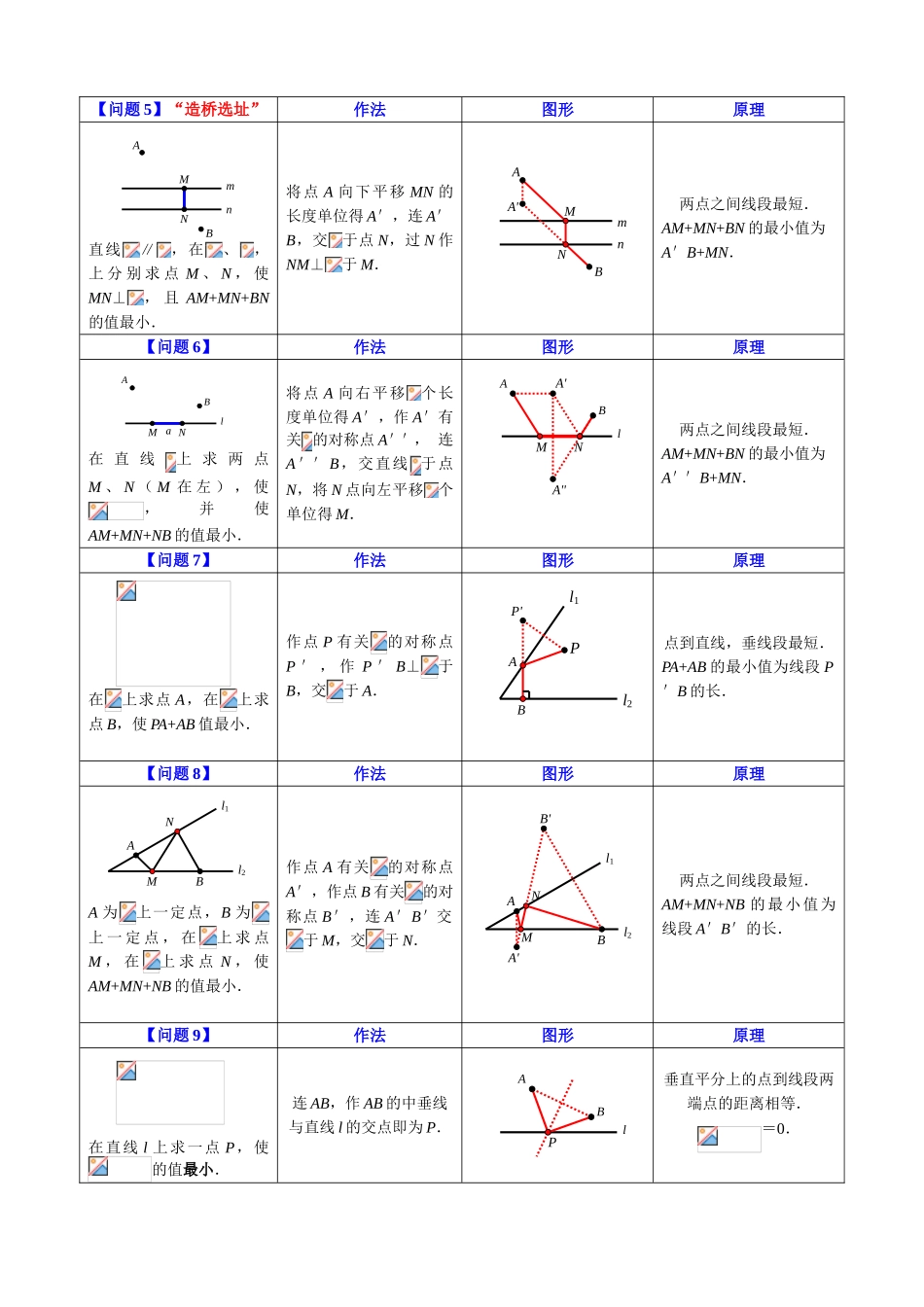
初中数学竞赛专题讲解最短途径问题【问题概述】最短途径问题是图论研究中的一种经典算法问题, 意在寻找图(由结点和途径构成的)中两结点之间的最短途径.算法详细的形式包括:① 确定起点的最短途径问题 - 即已知起始结点,求最短途径的问题.② 确定终点的最短途径问题 - 与确定起点的问题相反,该问题是已知终止结点,求最短途径的问题.③ 确定起点终点的最短途径问题 - 即已知起点和终点,求两结点之间的最短途径.④ 全局最短途径问题 - 求图中所有的最短途径.【问题原型】“将军饮马”,“造桥选址”,“费马点”.【波及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思绪】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考察.【十二个基本问题】【问题 1】作法图形原理在直线 l 上求一点 P,使PA+PB 值最小.连 AB,与 l 交点即为P.两点之间线段最短.PA+PB 最小值为 AB.【问题 2】“将军饮马”作法图形原理在直线 l 上求一点 P,使PA+PB 值最小.作 B 有关 l 的对称点 B'连 A B',与 l 交点即为P.两点之间线段最短.PA+PB 最小值为 A B'.【问题 3】作法图形原理在直线、上分别求点M、N,使△PMN 的周长最小.分别作点 P 有关两直线的对称点 P'和 P'',连 P'P'',与两直线交点即为 M,N.两点之间线段最短.PM+MN+PN 的最小值为线段 P'P''的长.【问题 4】作法图形原理在直线、上分别求点M、N,使四边形 PQMN的周长最小.分别作点 Q 、P 有关直线、的对称点 Q'和 P'连 Q'P',与两直线交点即为 M,N.两点之间线段最短.四边形 PQMN 周长的最小值 为 线 段 P ' P '' 的长.lPB'ABl1l2NMP''P'Pl1l2NMP'Q'QPl1l2PQ【问题 5】“造桥选址”作法图形原理直线∥,在、,上 分 别 求 点 M 、 N , 使MN⊥, 且 AM+MN+BN的值最小.将点 A 向下平移 MN 的长度单位得 A',连 A'B,交于点 N,过 N 作NM⊥于 M.两点之间线段最短.AM+MN+BN 的最小值为A'B+MN.【问题 6】作法图形原理在 直 线上 求 两 点M 、 N ( M 在 左 ) , 使,并使AM+MN+NB 的值最小.将点 A 向右平移个长度单位得 A',作 A'有关 的对称点 A'', 连A''B,交直线于...