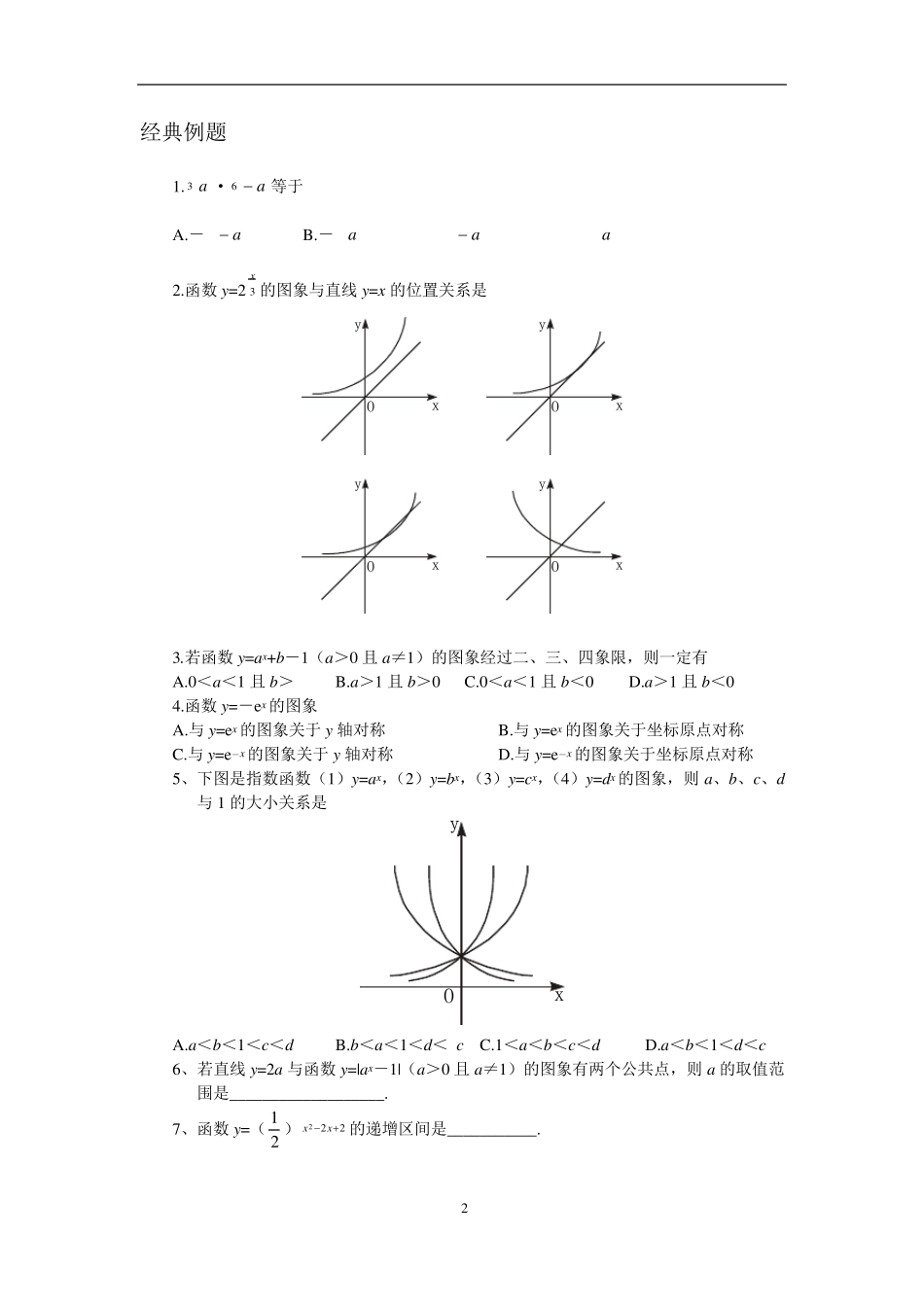
1 指数与指数函数 知识要点 1.指数 (1)n 次方根的定义:若xn=a,则称x 为a 的n 次方根,“ n”是方根的记号. 在实数范围内,正数的奇次方根是一个正数,负数的奇次方根是一个负数,0 的奇次方根是 0;正数的偶次方根是两个绝对值相等符号相反的数,0 的偶次方根是 0,负数没有偶次方根. (2)方根的性质 ①当 n 为奇数时,nna=a. ②当 n 为偶数时,nna=|a|=).0(),0(aaaa (3)分数指数幂的意义 ①a nm= nma(a>0,m、n 都是正整数,n>1). ②anm=nma1 =nma1(a>0,m、n 都是正整数,n>1). 2.指数函数 (1)指数函数的定义 一般地,函数y=ax(a>0 且 a≠1)叫做指数函数. (2)指数函数的图象 Ox yOx yy=a x 11a> )1y=a x ( (0<a<1) 底数互为倒数的两个指数函数的图象关于 y 轴对称. (3)指数函数的性质 ①定义域:R . ②值域:(0,+∞). ③过点(0,1),即 x=0 时,y=1. ④当 a>1 时,在 R 上是增函数;当 0<a<1 时,在 R 上是减函数. 2 经典例题 1. 3 a · 6a等于 A.-a B.-a C. a D. a 2.函数 y=2 3x的图象与直线 y=x 的位置关系是 Ox yOx yOx yOx yA B C D 3.若函数 y=ax+b-1(a>0 且 a≠1)的图象经过二、三、四象限,则一定有 A.0<a<1 且 b> B.a>1 且 b>0 C.0<a<1 且 b<0 D.a>1 且 b<0 4.函数 y=-ex的图象 A.与 y=ex的图象关于 y 轴对称 B.与 y=ex的图象关于坐标原点对称 C.与 y=e-x的图象关于 y 轴对称 D.与 y=e-x的图象关于坐标原点对称 5、下图是指数函数(1)y=ax,(2)y=bx,(3)y=cx,(4)y=dx的图象,则 a、b、c、d与 1 的大小关系是 Oxy1(1) (2) (3) (4) A.a<b<1<c<d B.b<a<1<d< c C.1<a<b<c<d D.a<b<1<d<c 6、若直线 y=2a 与函数 y=|ax-1|(a>0 且 a≠1)的图象有两个公共点,则 a 的取值范围是___________________. 7、函数 y=( 21 )222 xx的递增区间是___________. 3 8、 已知2xx 2≤(41 )x-2,求函数y=2x-2-x的值域. 9、要使函数y=1+2x+4xa 在x∈(-∞,1]上y>0 恒成立,求a 的取值范围 . 基础练习 1、已知f(x)=ax,g(x)=-lo gbx,且lga+lgb=0,a≠1,b≠1,则y=f(x)与y=g(x)的图象( ) A.关于直线x+y=0 对称 B.关于直线x-y=0 对称 C.关于y轴...